Home
Class 12
PHYSICS
A particle which is constant to move alo...

A particle which is constant to move along the `x- axis` , is subjected to a force in the same direction which varies with the distance `x` of the particle from the origin as `F(x) = -Kx + ax^(3)` . Hero `K` and `a` are positive constant . For `x ge 0`, the fanctional from of the patential every `U(x) of the particle is

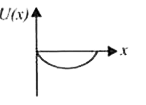
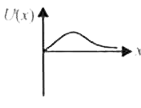
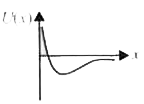
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
D
Given, `F(x) = - kx + ax^(3)" "…(i)`
`rArr dU= -F dx` or `U(x) =-int_(0)^(x) (-kx + ax^(3) ) dx`
`rArr U(x) = (kx^(2))/( 2) - (ax^(4))/( 4) " "…(ii)`
From eqn. (ii) , `U(x) =0`
`rArr (kx^(2) ) /( 2) (1- (ax^2)/( 2k) )=0`
`rArr x=0 and x= pm sqrt((2k)/( a))`.
Also, `U(x) =` negative for `x gt sqrt((2k)/( a))`
Now finding points where force is zero
`x(-k + ax^(2) ) = 0`
or `x=0 and x= pm sqrt((k)/( a))`
The slope of U-x graph is zero at these points. Therefore, the most appropriate option is (d).
Promotional Banner

Topper's Solved these Questions

  • WORK, POWER, ENERGY

    MTG-WBJEE|Exercise EXERCISE (WB JEE WORKOUT) CATEGORY 3 : One or More than One Option Correct Type (2 Marks)|10 Videos

  • WORK, POWER, ENERGY

    MTG-WBJEE|Exercise EXERCISE (WB JEE Previous Years Questions) CATEGORY 1 : Single Option Correct Type (1 Mark)|3 Videos

  • WORK, POWER, ENERGY

    MTG-WBJEE|Exercise EXERCISE (WB JEE Previous Years Questions) CATEGORY 1 : Single Option Correct Type (1 Mark)|3 Videos

  • WAVE OPTICS

    MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTION (MCQ.s)|9 Videos

Similar Questions

Explore conceptually related problems

A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F (x) =-kx + ax^(3) . Here, k and a are positive constants. For x(ge0, the functional form of the potential energy (u) U of the U (x) the porticle is. (a) , (b) , (c) , (d) .

A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x) = -kx + ax^(3) . Here k and a are origin as F(x) = -kx + ax^(3) . Here k and a are positive constants. For x=0 , the functional form of the potential energy U(x) of particle is.

The kinetic energy of a particle moving along x-axis varies with the distance x of the particle from origin as K=(A+x^3)/(Bx^(1//4)+C) .Write the dimensional formula for A^2B

A force F=-k/x_2(x!=0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x = + a to x = 2a . Here, k is a positive constant.

A particle moving along the x- axis is subjected to a force given by F=F_(0)(e^(x//a)-1) where F_(0) and are constants Determine an expression for the work done by this force as the particle moves from the origin to the point x=r

A particle free to move along x-axis is acted upon by a force F=-ax+bx^(2) whrte a and b are positive constants. For ximplies0 , the correct variation of potential energy function U(x) is best represented by.

A particle constrained to move along the x-axis in a potential V=k"x"^(2) is subjected to an external time dependent force vec(f)(t) here k is a constant, x the distance from the origin, and t the time. At some time T, when the particle has zero velocity at x = 0, the external force is removed. Choose the incorrect options – (1) Particle executes SHM (2) Particle moves along +x direction (3) Particle moves along – x direction (4) Particle remains at rest