Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
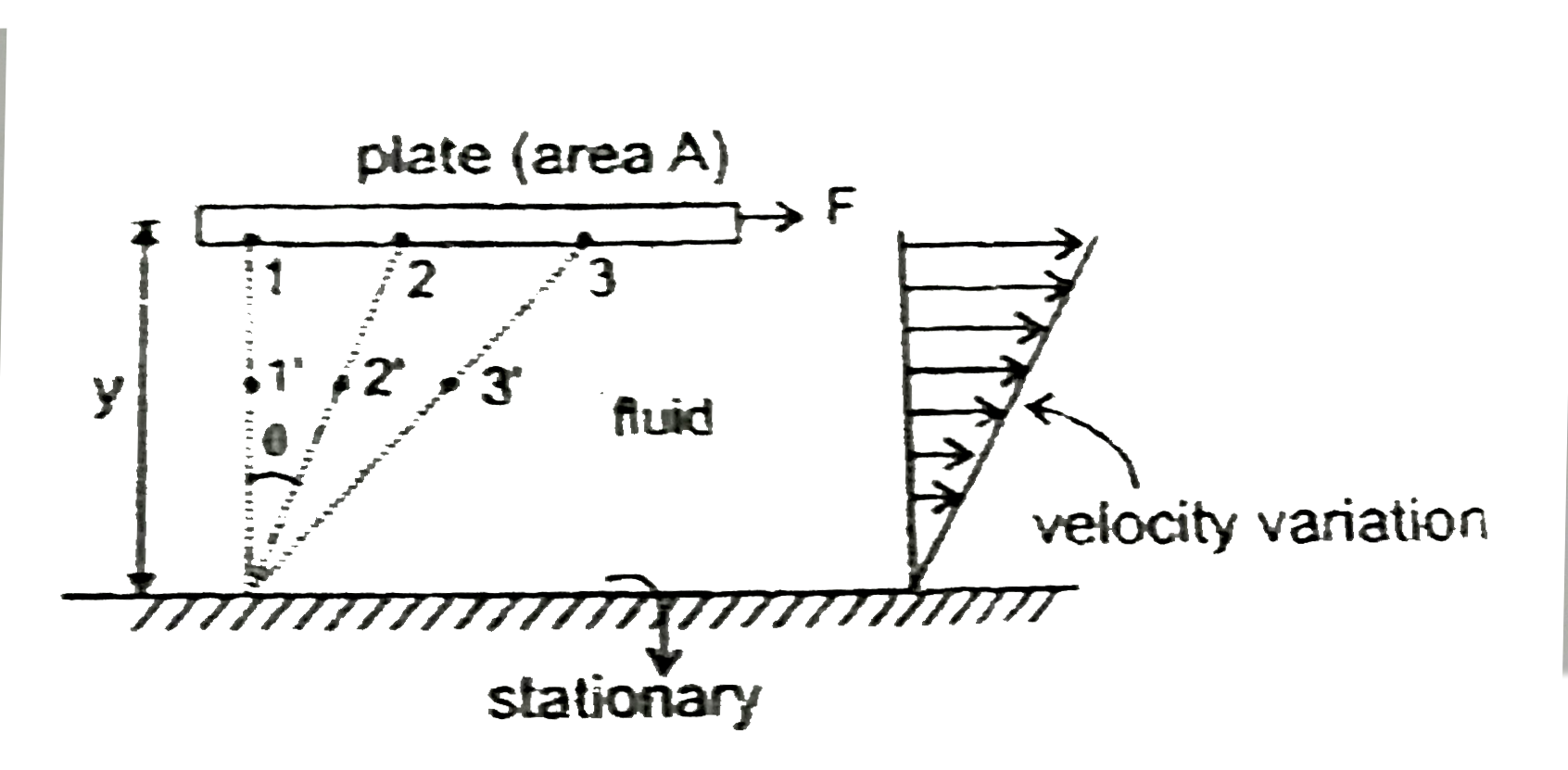
In the given figure as the the plate moves the fluid particle at the surface moves from position `1` to `2` and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
`(F)/(A) alpha(d' theta)/(dt)` but `y(d' theta)/(dt)=u,(d' theta)/(dt) = (u)/(y)`
then `F = eta A(u)/(y), eta =` coefficient of viscosity
for non-linear velocity distribution -
`F = eta A(du)/(dy)`
where `(u)/(y)` or `(du)/(dy)` is known as velocity gradiant.
In previous question the value of constant speed of palte `(m//sec.)` is equal to
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
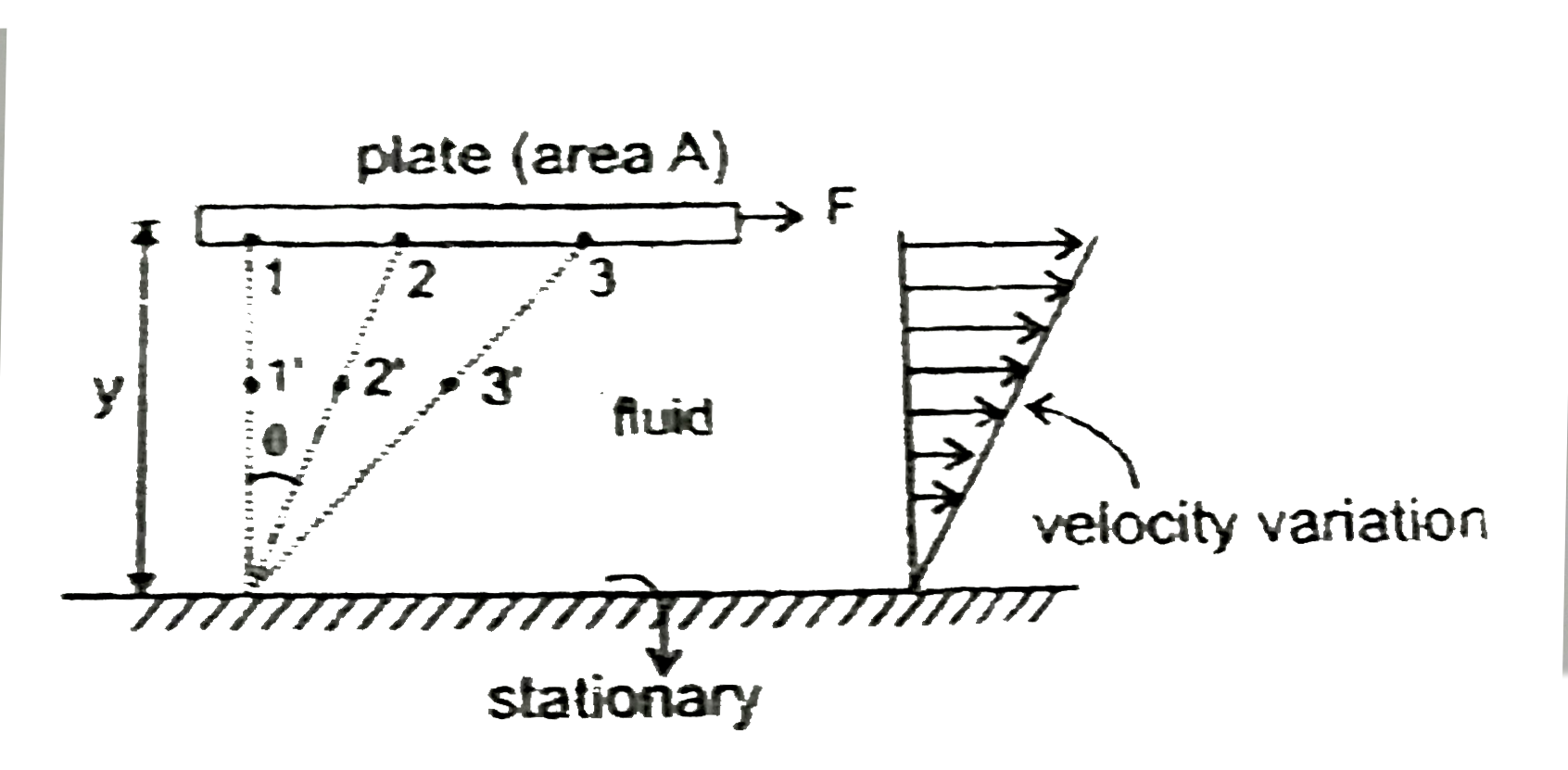
In the given figure as the the plate moves the fluid particle at the surface moves from position `1` to `2` and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
`(F)/(A) alpha(d' theta)/(dt)` but `y(d' theta)/(dt)=u,(d' theta)/(dt) = (u)/(y)`
then `F = eta A(u)/(y), eta =` coefficient of viscosity
for non-linear velocity distribution -
`F = eta A(du)/(dy)`
where `(u)/(y)` or `(du)/(dy)` is known as velocity gradiant.
In previous question the value of constant speed of palte `(m//sec.)` is equal to
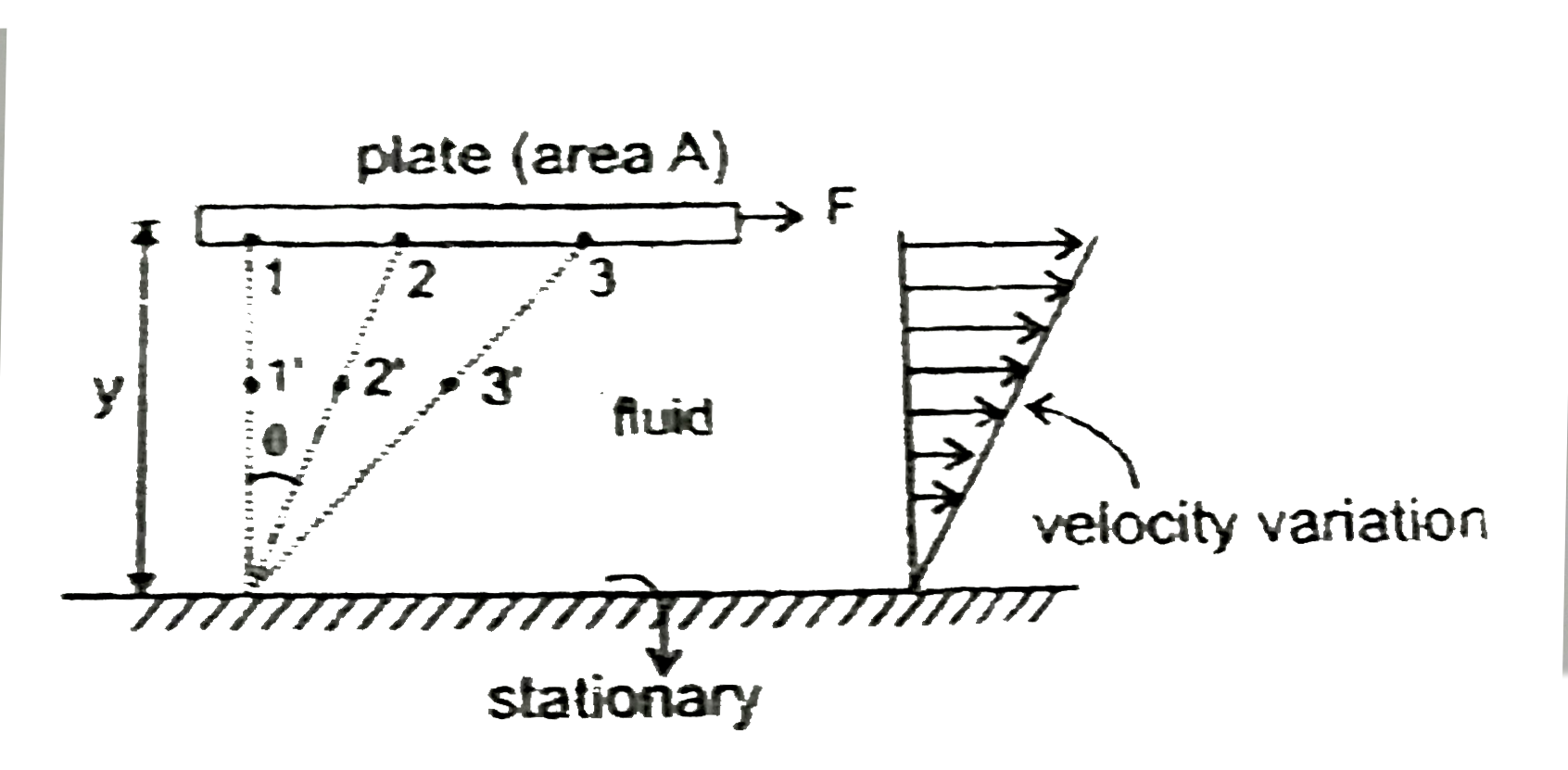
In the given figure as the the plate moves the fluid particle at the surface moves from position `1` to `2` and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
`(F)/(A) alpha(d' theta)/(dt)` but `y(d' theta)/(dt)=u,(d' theta)/(dt) = (u)/(y)`
then `F = eta A(u)/(y), eta =` coefficient of viscosity
for non-linear velocity distribution -
`F = eta A(du)/(dy)`
where `(u)/(y)` or `(du)/(dy)` is known as velocity gradiant.
In previous question the value of constant speed of palte `(m//sec.)` is equal to
Similar Questions
Explore conceptually related problems
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. The velocity gradient just near the bottom boundary is equal to -
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. The velocity gradient just near the bottom boundary is equal to -
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. The velocity gradient just below the plate, in above problem is equal to - (per second)
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. The velocity gradient just below the plate, in above problem is equal to - (per second)
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. In the given figure if force of 2N required to maintain constant velocity of plate, the value of constant C_(1), & C_(2) are -
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. In the given figure if force of 2N required to maintain constant velocity of plate, the value of constant C_(1), & C_(2) are -
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. If velocity distribution is given as (parabolic) u = c_(1)y^(2) + c_(2)y + c_(3) For the same force of 2N and the speed of the plate 2 m//sec , and area of plate is 1 and viscousity is .001, the constant C_(1), C_(2) & C_(3) are
Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. If velocity distribution is given as (parabolic) u = c_(1)y^(2) + c_(2)y + c_(3) For the same force of 2N and the speed of the plate 2 m//sec , the constant C_(1), C_(2) & C_(3) are
Viscosity In Fluid
State Newton's law of viscosity of fluids in motion.
Recommended Questions
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Assertion: The flow of fluid is said to be steady if at any given poin...
Text Solution
|
- Assertion: The shape of an automobile is so designed that its front re...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- The coefficient of viscosity n of a fluid moving steadily between two ...
Text Solution
|