Similar Questions
Explore conceptually related problems
Recommended Questions
- A projectile is fired from the base of cone shaped hill. The projecti...
Text Solution
|
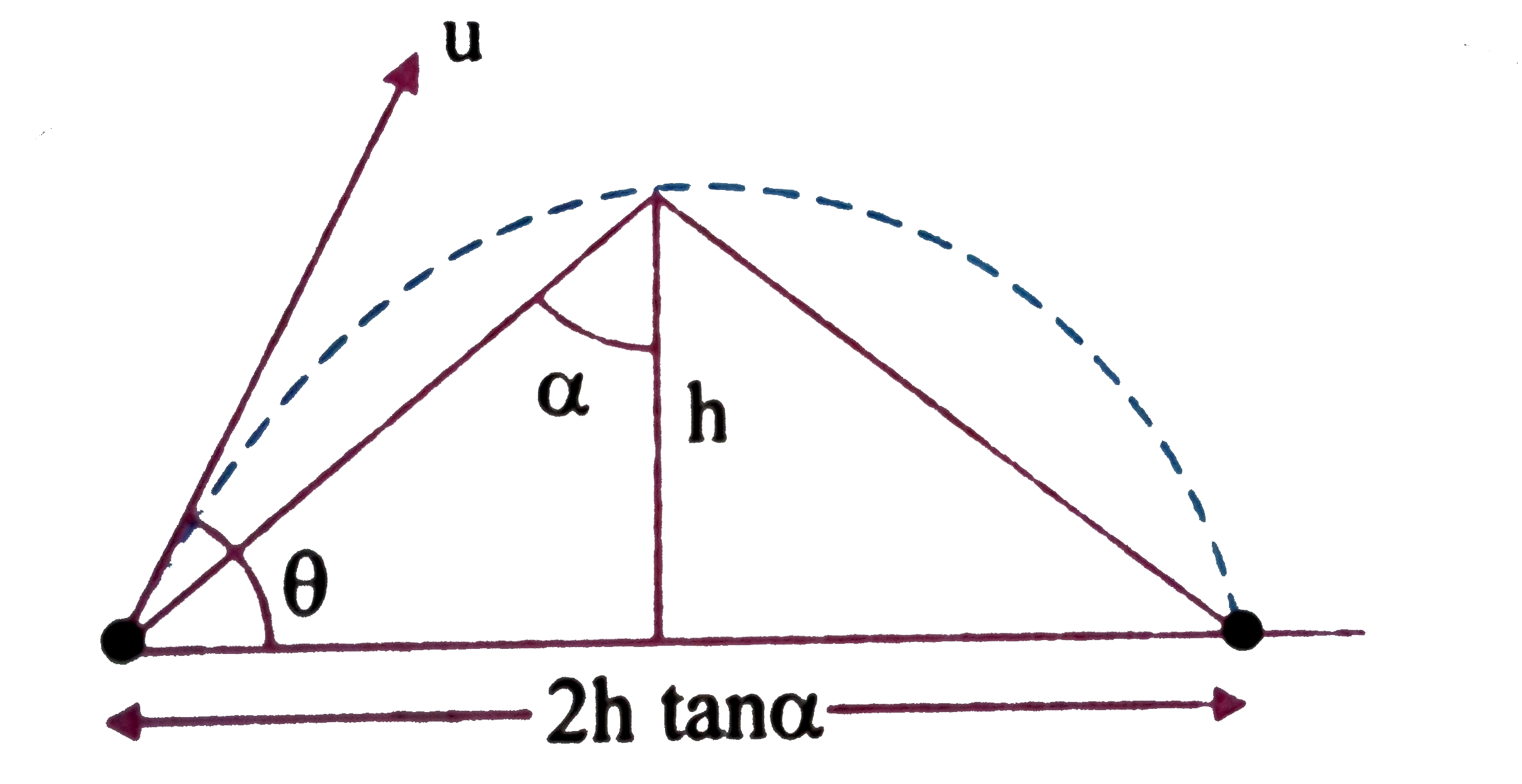
- A shot is fired at an angle theta to the horizontal such that it strik...
Text Solution
|
- A projectile is fired from the base of coneshaped hill. The projectil...
Text Solution
|
- A projectile fired with initial velocity u at some angle theta has a r...
Text Solution
|
- A projectile is fired from the base of cone shaped hill. The projectle...
Text Solution
|
- एक प्रक्षेप्य को क्षैतिज से theta कोण पर कुछ प्रारम्भिक वेग v से फेंक...
Text Solution
|
- एक प्रक्षेप्य u वेग से क्षैतिज से 2theta कोण पर प्रक्षेपित किया जाता ह...
Text Solution
|
- A projectile with an initial velocity u and a projection angle theta i...
Text Solution
|
- The velocity at the maximum height of a projectile is half of its init...
Text Solution
|