Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass 1.5 kg moves along x-axis in a conservative force f...
Text Solution
|
- The potential energy of a particle executing SHM along the x-axis is g...
Text Solution
|
- A particle of mass 1.5 kg moves along x-axis in a conservative force f...
Text Solution
|
- A particle of mass 1.5 kg moves along x-axis in a conservative force f...
Text Solution
|
- A particle of mass 1.5 kg moves along x-axis in a conservative force f...
Text Solution
|
- A single conservative f((x)) acts on a m = 1 kg particle moving along ...
Text Solution
|
- A single conservative force F(x) acts on a particle that moves along t...
Text Solution
|
- A single conservative force F(x) acts on particle that moves along the...
Text Solution
|
- A particle is executing simple harmonic motion (SHM) of amplitude A, a...
Text Solution
|
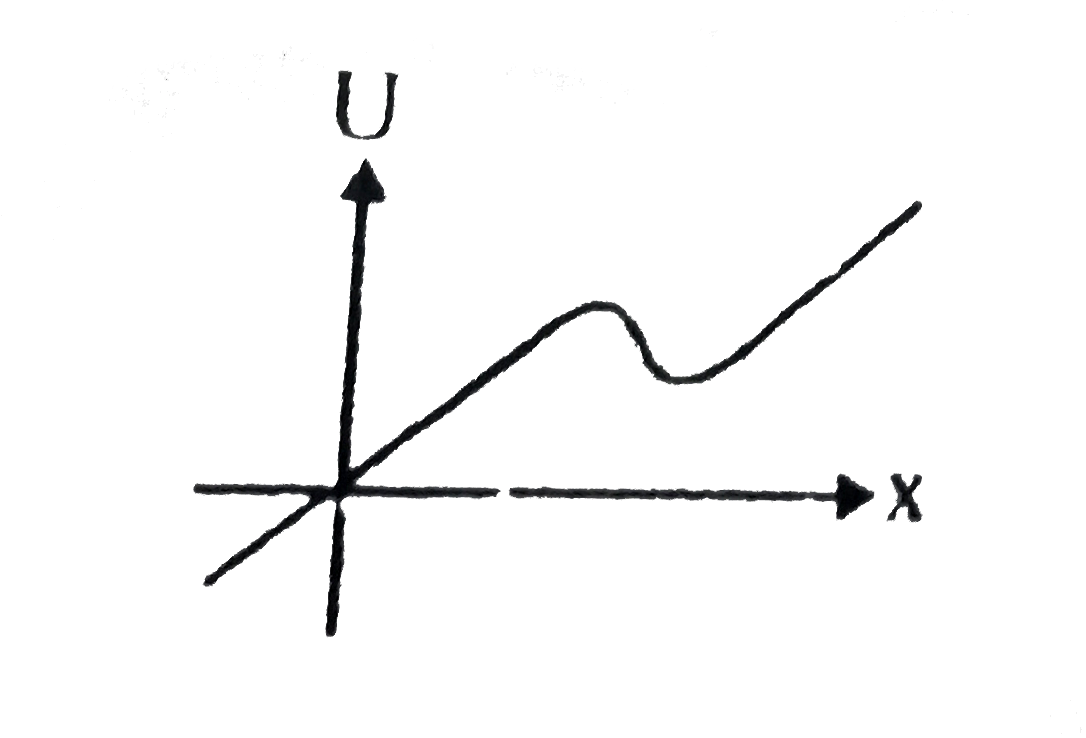 It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the value of `x_(0)` ?
It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the value of `x_(0)` ?