Similar Questions
Explore conceptually related problems
Recommended Questions
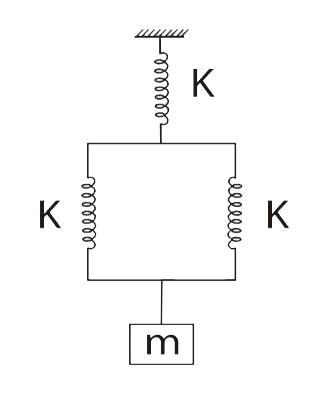
- A body of mass 'm' hangs from three springs, each of spring constant '...
Text Solution
|
- A block of mass m hangs from a vertical spring of spring constant k. I...
Text Solution
|
- A particle of mass 'm' is attached to three identical springs A,B and ...
Text Solution
|
- A body of mass m is suspended from three springs as shown in figure. I...
Text Solution
|
- A body of mass m = 2kg hangs from three springs, each of spring consta...
Text Solution
|
- The period of oscillation of a mass M suspended from a spring of sprin...
Text Solution
|
- A body of mass 'm' hangs from three springs, each of spring constant '...
Text Solution
|
- m द्रव्यमान का एक पिण्ड एक स्प्रिंग से बँधा हुआ है और दोलन करता है। यद...
Text Solution
|
- A block of mass m hangs from three springs having same spring constant...
Text Solution
|