Similar Questions
Explore conceptually related problems
Recommended Questions
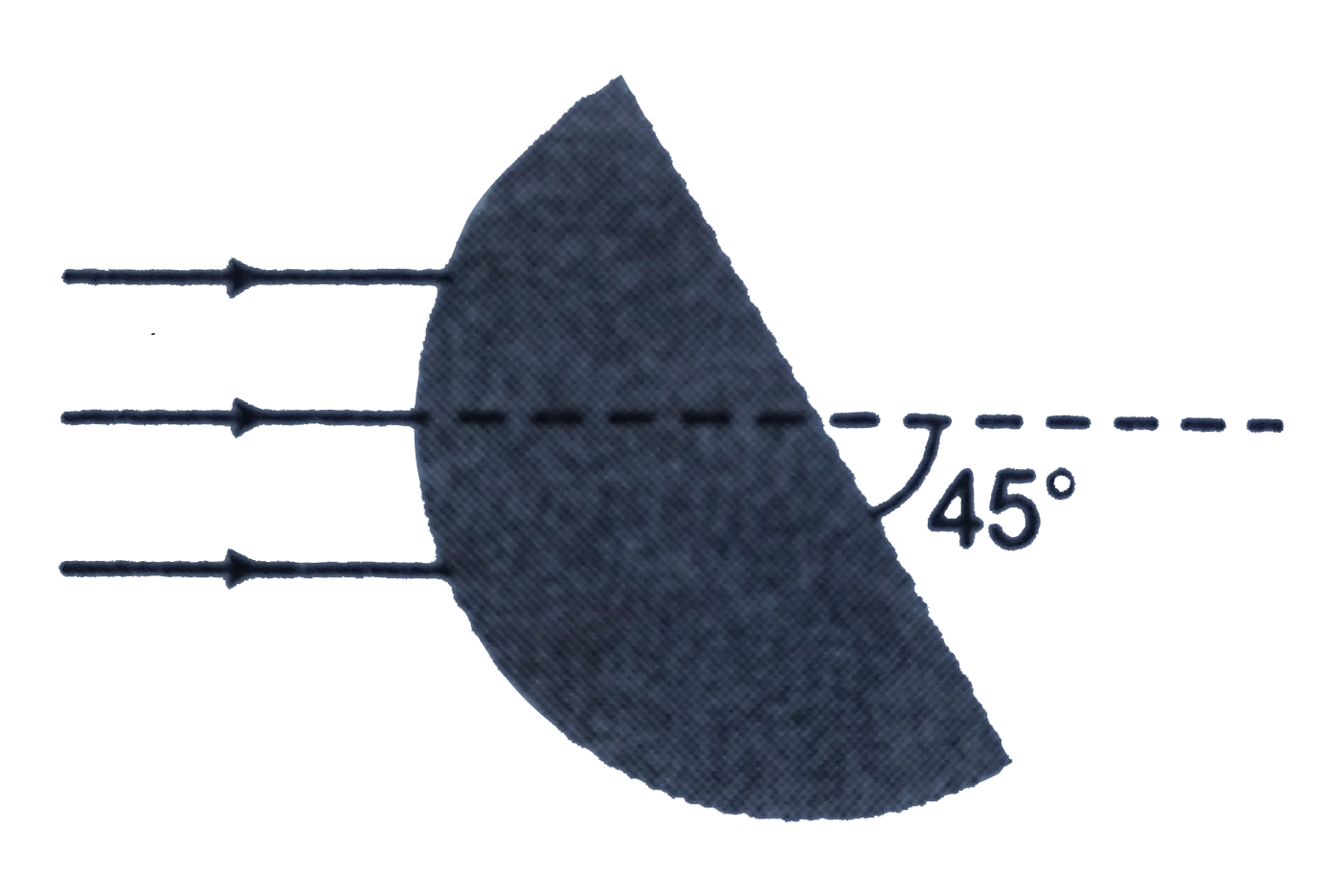
- A parallel narrow beam of light is incident on the surface of a transp...
Text Solution
|
- Figure shows a transparent hemisphere of radius 3'0 cm made of a mate...
Text Solution
|
- A parallel narrow beam of light is incident on the surface of a transp...
Text Solution
|
- A parallel beam of light travelling in water (refractive index =4//3) ...
Text Solution
|
- A small point objects is placed in air at a distance of 60 cm from a c...
Text Solution
|
- A parallel beam of light is incident on the surface of a transparent h...
Text Solution
|
- A narrow parallel beam of light falls on a glass sphere of radius R an...
Text Solution
|
- Parallel rays of light are falling on convex sphere surface of radius ...
Text Solution
|
- AN unpolarised beam of light is incident at the polarising angle on th...
Text Solution
|