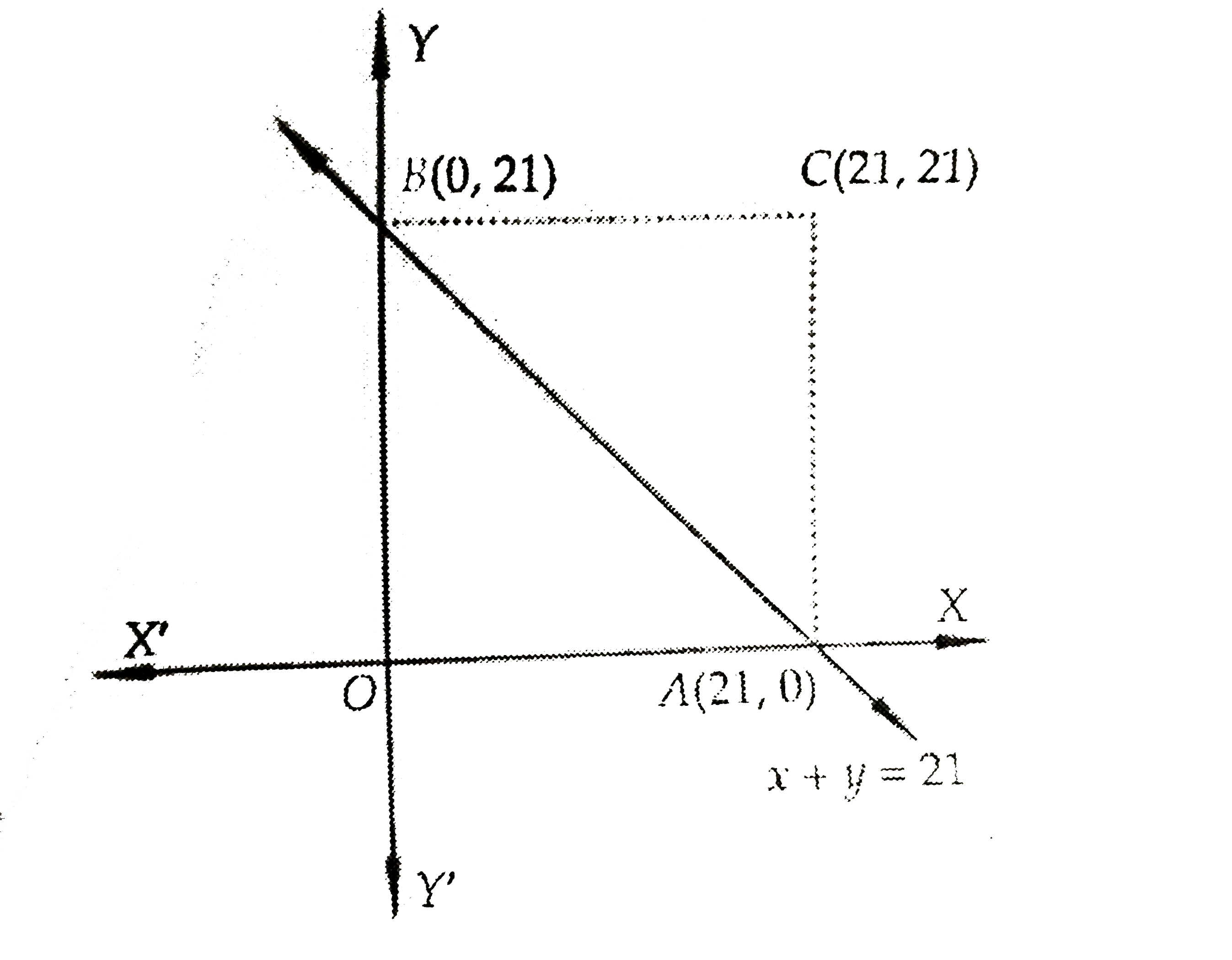A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Number of integral points (integral points means both the co-ordinates...
Text Solution
|
- Number of integral points (integral points means both the co-ordinates...
Text Solution
|
- The number of points, having both coordinates are integers, that lie i...
Text Solution
|
- The number of points, having both co-ordinates as integers, that lie i...
Text Solution
|
- Number of points with integral co-ordinates that lie inside a triangle...
Text Solution
|
- The number of points, having both co-ordinates as integers, that lie i...
Text Solution
|
- Find the number of points , having both co- ordinates as integers , th...
Text Solution
|
- Find the number of points , having both co- ordinates as integers , th...
Text Solution
|
- The number of integral points (integral point means both the coordinat...
Text Solution
|