Similar Questions
Explore conceptually related problems
Recommended Questions
- Four point masses easch of mass 'm' are placed at four vertieces A, B,...
Text Solution
|
- Three point masses 'm' each are kept at three verties of a square pf s...
Text Solution
|
- Four point masses easch of mass 'm' are placed at four vertieces A, B,...
Text Solution
|
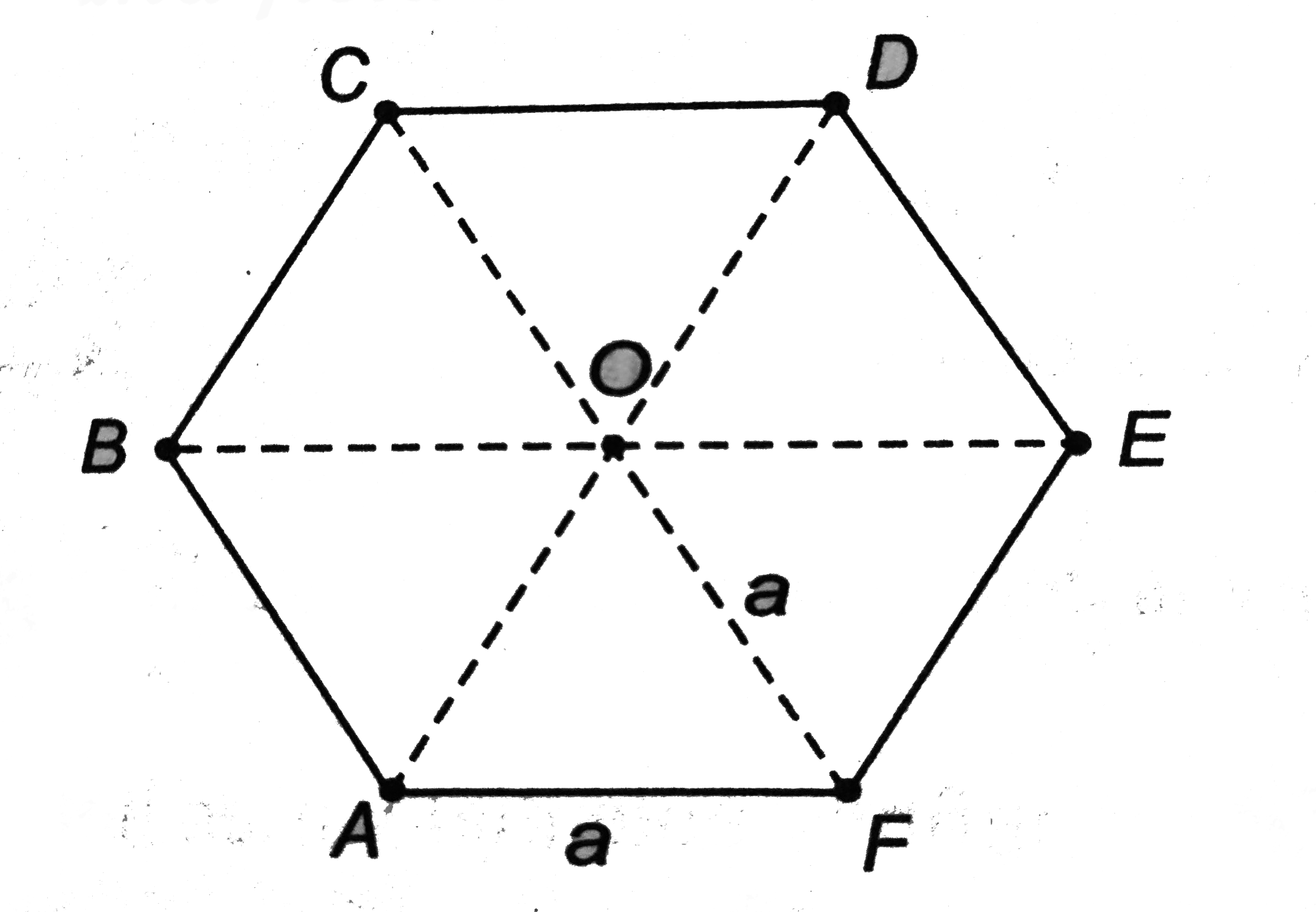
- Six particles each of massm are placed at the corners of a regular hex...
Text Solution
|
- Find the position of centre of mass for a system of particles places a...
Text Solution
|
- Assertion : Four point masses each of mass m are placed at points 1, 2...
Text Solution
|
- Six point charges are arrange at the vertices of a regular hexagon of ...
Text Solution
|
- Four identical masses m each are kept at points A, B, C & D shown in f...
Text Solution
|
- Find the potential energy of a charge q(0) placed at the centre of reg...
Text Solution
|
 .
.