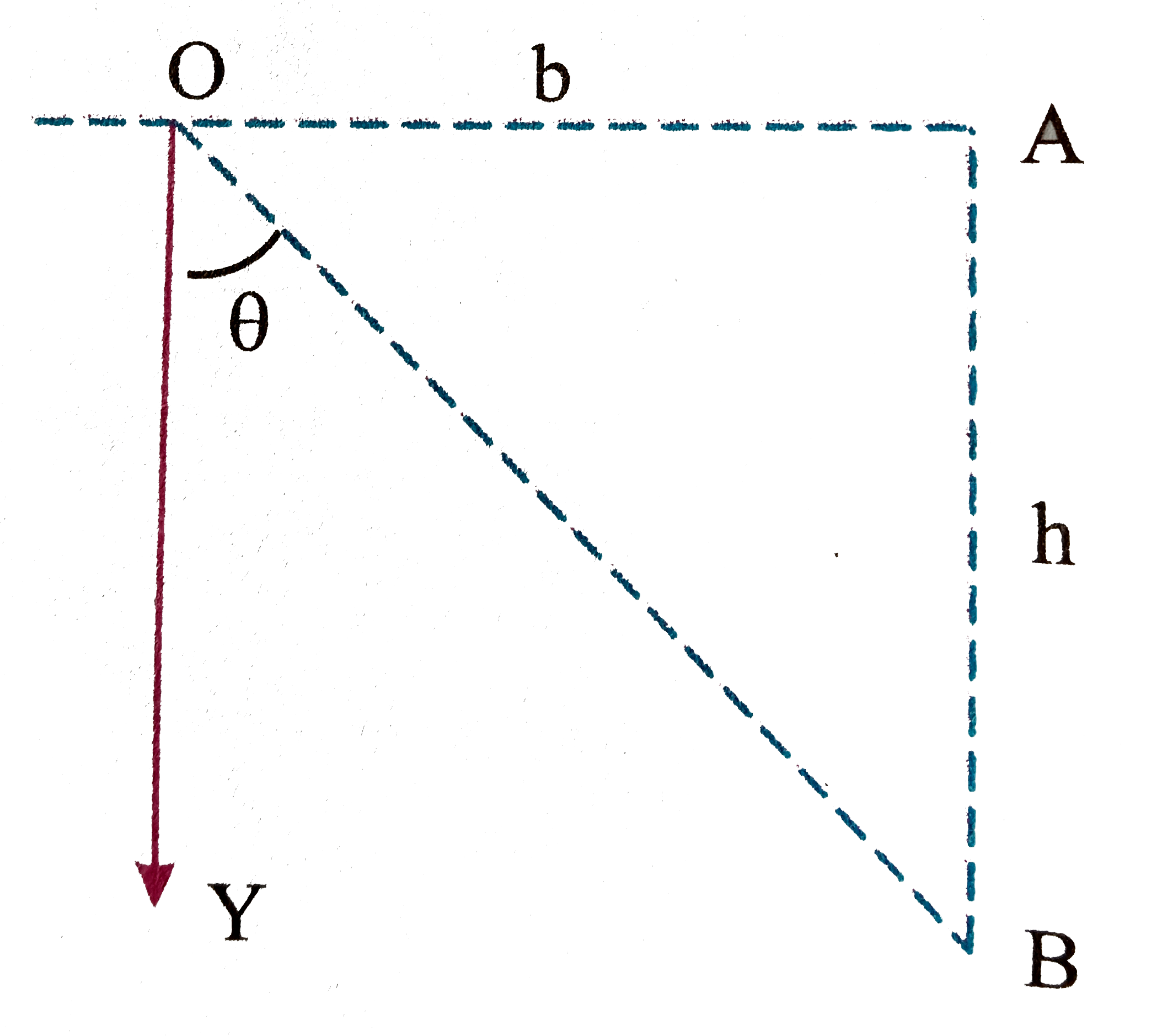
A particle of mass `m` is released from rest at point `A` in the figure falling freely under gravity parallel to the vertical `Y`-axis. The magnitude of angular momentum of particle about point `O` when it reaches `B` is (where `OA=b` and `AB=h`)

A particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y -axis. Find the angular momentum of the particle at any time t with respect to the same origin O .

A particle mass 1 kg is moving along a straight line y=x+4 . Both x and y are in metres. Velocity of the particle is 2m//s . Find the magnitude of angular momentum of the particle about origin.

A particle of mass m is released in vertical plane from a point P at x=x_(0) on the x -axis. It falls vertically parallel to the y -axis. Find the torque tau acting on the particle at a time about origin.

A particle of mass 1 kg is moving alogn the line y=x+2 with speed 2m//sec . The magnitude of angular momentum of the particle about the origin is

A particle of mass m is projected with a velocity v making an angle of 45^@ with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.

A particle of mass "m" is projected with a velocity ' "u" ' making an angle of 30^(@) with the horizontal. The magnitude of angular momentum of the projectile about the point of projection when the particle is at its maximum height "h" is :

A partricle of mass m is projected with a velocity v at an angle of 60^(@) with horizontal When the particle is at the maximum height. The magnitude ofits angular momentum about the point ofprojection is

A particle of mass m is projected from the ground with an initial speed u at an angle alpha . Find the magnitude of its angular momentum at the highest point of its trajector about the point of projection.

In Fig. 10-73, a particle of mass m is released from rest at point A, at distance b from the origin, and falls parallel to a vertical y axis. As a function of time t and with respect to the origin, find the magnitudes of (a) the torque tau on the particle due to the gravitational force and (b) the angular momentum L of the particle. ( c) From those results, verify that tau=dL//dt .