In each situation we can relate the acceleration `vec(a)` to the net force `vec(F)_("net")` acting on the puck with Newton.s second law, `vec(F)_("net")=m vec(a)`. However, because the motion is along only the x axis, we can simplify each situation by writing the second law for x components only:
`F_("net.x")=ma_(x)." "(5-4)`
The free-body diagrams for the three situations are also given in Fig. 5-3, with thee puck represented by a dot.
Calculations :
Situation A: Foor Fig. 5-3b, where only one horizontal force acts, Eq. 5-4 gives us
`F_(1)=ma_(x)`,
which, with given data, yields
`a_(x)=(F_(1))/(m)=(4.0N)/(0.20kg)=20" m"//"s"^(2)`.
The positive answer indicates that the acceleration is in the positive direction of the x axis.
Situation B: In Fig. 5-3d, two horizontal forces act on the puck, `vec(F)_(1)` in the positive direction of x and `vec(F)_(2)` in the negative direction. Now Eq. 5-4 gives us
`F_(1)-F_(2)=ma_(x)`,
which, with given data, yields
`a_(x)=(F_(1)-F_(2))/(m)=(4.0N-2.0N)/(0.20kg)=10" m"//"s"^(2)`.
Thus, the net force accelerates the puck in the positive direction of the x axis.
Situation C: In Fig. 5-3f, force `vec(F)_(3)` is not directed along the direction oof the puck.s acceleration, only x component `F_(3,x)` is. (Force `vec(F)_(3)` is two-dimensional but the motion is only one-dimensional.) Thus, we write Eq. 5-4 as
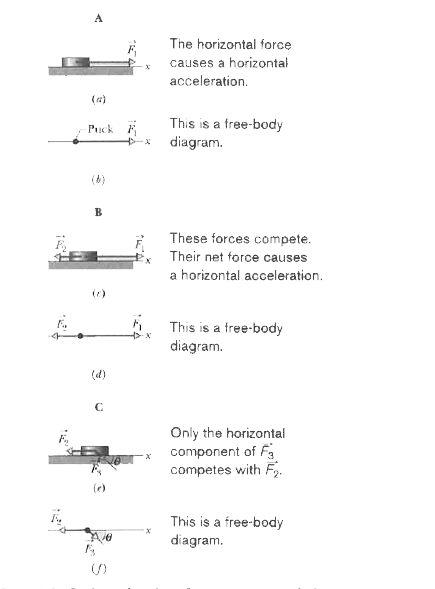
Figure 5-3 In three situations, forces act on a puck that moves along an x axis. Free-body diagrams are also shown.
`F_(3,x)-F_(2)=ma_(x)." "(5-5)`
From the figure, we see that `F_(3,x)=F_(3)cos theta`. Solving for the acceleration and substituting for `F_(3,x)` yield
`a_(x)=(F_(3,x)-F_(2))/(m)=(F_(3)cos theta-F_(2))/(m)`
`=((1.0N)(cos 30^(@))-2.0N)/(0.20kg)=-5.7" m"//"s"^(2).`
Thus, the net force accelerates the puck in the negative direction of the x axis.
