The net force `vec(F)_("net")` on the tin is the sum of the tree forces and is related to the acceleration `vec(a)` via Newton.s second law `(vec(F)_("net")=m vec(a))`. Thus,
`vec(F)_(1)+vec(F)_(2)+vec(F)_(3)=m vec(a)," "(5-6)`
which gives us
`vec(F)_(3)=m vec(a)-vec(F)_(1)-vec(F)_(2)." "(5-7)`
Calculations: Because this is a two-dimensional problem, we cannot find `vec(F)_(3)` merely by substituting the magnitudes for the vector quantities on the right side of Eq. 5-7. Instead, we must vectorially add `m vec(a),-vec(F)_(1)` (the reverse of `vec(F)_(1)`), and `-vec(F)_(2)` (the reverse of `vec(F)_(2)`), as shown in Fig. 5-4b. This addition can be done directly on a vector-capable calculator because we know both magnitude and angle for all three vectors. However, here we shall evaluate the right side of Eq. 5-7 in terms of components, first along the x axis and then along the y axis. Caution: Use only one axis at a time.
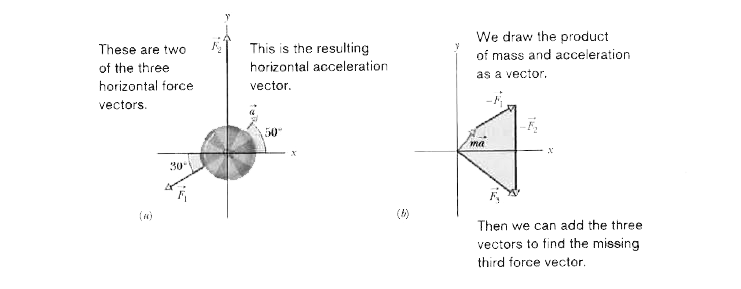
Figure 5-4 (a) An overhead view of two three horizontal forces that act on a cookie tin, resulting in acceleration `vec(a).vec(F)_(3)` is not shown. (b) An arrangement of vectors `m vec(a),-vec(F)_(1)`, and `-vec(F)_(2)` to find force `vec(F)_(3)`.
x components: Along the x axis we have
`F_(3,x)=ma_(x)=F_(1,x)-F_(2,x)`
`=m(a cos 50^(@))-F_(1)cos(-150^(@))-F_(2)cos90^(@)`.
Then, substituting known data, we find
`F_(3,x)=(2.0" kg")(3.0" m"//"s"^(2))cos 50^(@)-(10" N")cos(-150^(@))`
`-(20" N")cos 90^(@)`
`=12.5` N.
y comonents: Similarly, along the y axis we find
`F_(3,y)=ma_(y)-F_(1,y)-F_(2,y)`
`=m(a sin 50^(@))-F_(1)sin(-150^(@))-F_(2)sin 90^(@)`
`=(2.0" kg")(3.0" m"//"s"^(2))sin 50^(@)-(10" N")sin(-150^(@))`
`-(20" N")sin 90^(@)`
`=10.4" N"`.
Vector: In unit-vector notation, we can write
`vec(F)_(3)=F_(3,x)hati+F_(3,y)hatj=(12.5" N")hati-(10.4" N")hatj`
`~~(13" N")hati-(10" N")hatj`.
We can now use a vector-capable calculator to get the magnitude and the angle of `vec(F)_(3)`. We can also use Eq. 3-6 to obtaiin the magnitude and the angle (from the positive direction of the x axis) as
`F_(3)= sqrt(F_(3,x)^(2)+F_(3,y)^(2))=16" N"`
and `" "theta=tan^(-1)(F_(3,y))/(F_(3,x))=-40^(@)`.
