The free-body diagram for each block is shown in Fig. 5-33. T is the tension in the cord and `theta=30^(@)` is the angle of the incline. For block 1, we take the +x direction to be up the incline and the +y direction to be in the direction
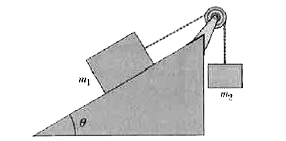
Figure 5-32 Block on frictionless inclined plane connected by a cord over a pulley to another block.
of the normal force `vec(F)_(N)` that the plane exerts on the block. For block 2, we take the +y direction to be down.
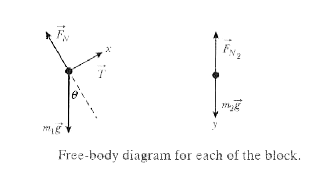
Figure 5-33 Free-body diagram for each of the block.
In this way, the accelerations of the two blocks can be represented by the same symbol a, without ambiguity Applying Newton.s second law to the x and y axes for block 1 and to the y axis of block 2, we obtain
`T-m_(1)g sin theta=m_(1)a" "(5-41)`
`F_(N)-m_(1)g cos theta =0" "(5-42)`
`m_(2)g-T=m_(2)a" "(5-43)`
respectively. The first and third of these equations provide a simultaneous set for obtaining values of a and T. The second equation is not needed in this problem, since the normal force is neither asked for nor is it needed as part of some further computation (such as can occur in formulas for friction).
Calculation:: We add Eqs. (5-41) and (5-43) above:
`m_(2)g-m_(1)g sin theta=m_(1)a+m_(2)a.`
Consequently, we find
`a=((m_(2)-m_(1)sin theta)g)/(m_(1)+m_(2))`
`=([2.30" kg"-(3.70" kg")sin 30.0^(@)](9.80" m"//"s"^(2)))/(3.70" kg"+2.30" kg")`
`=0.735" m"//"s"^(2)`
(b) What is the direction of the acceleration of the hanging block ?
Reasoning: The result for a is positive, indicating that the acceleration of block 1 is indeed up the incline and that the acceleration of block 2 is vertically down.
( c ) What is the tension in the cord?
Calculation: The tension in the cord is
`T=m_(1)a+m_(1)g sin theta`
`=(3.70" kg")(0.735" m"//"s"^(2))+(3.70" kg")(9.80" m"//"s"^(2))sin 30.0^(@)`
`=20.8" N"`.

