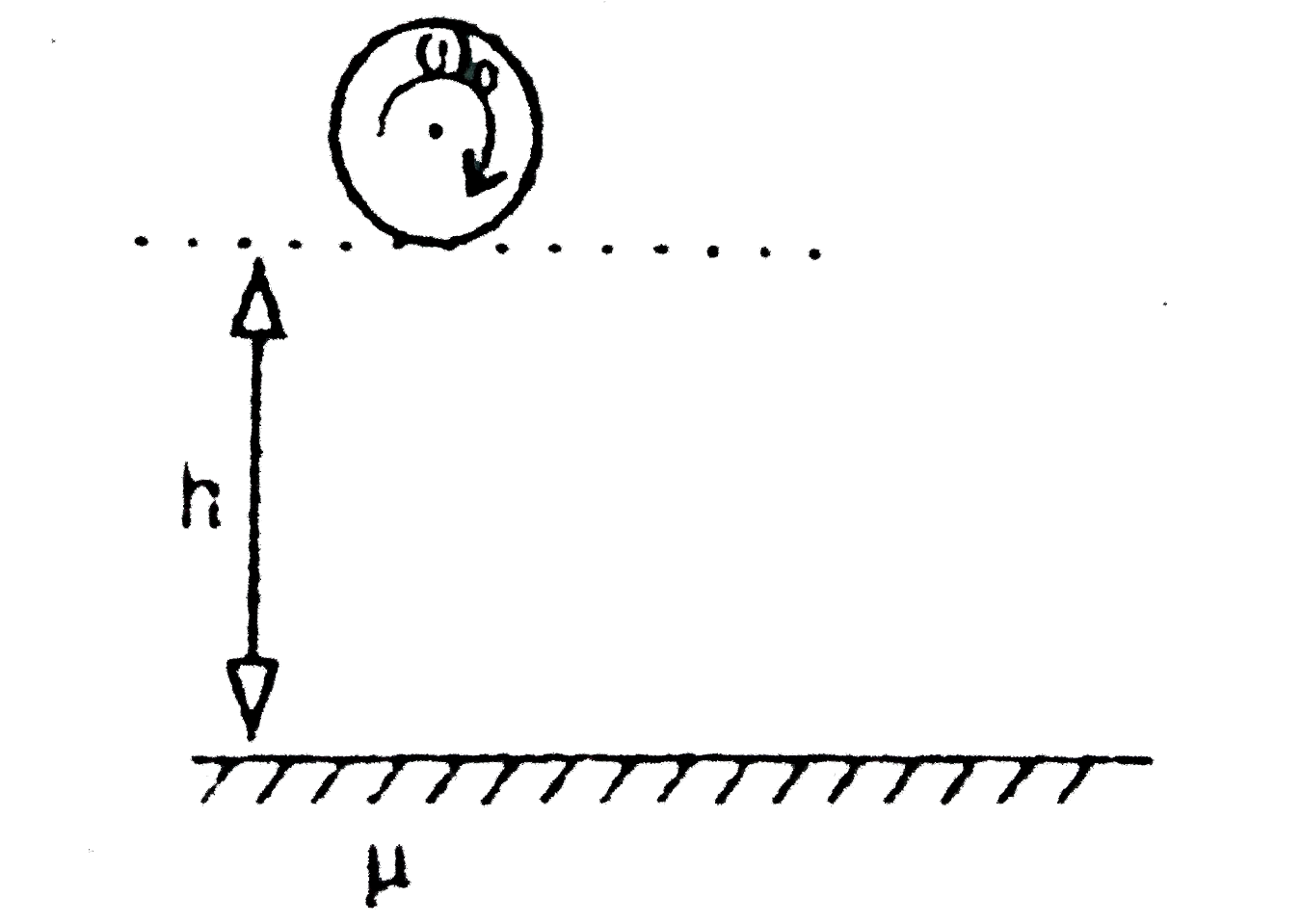Similar Questions
Explore conceptually related problems
Recommended Questions
- A solid sphere with angular velocity omega(0) is dropped on a rough su...
Text Solution
|
- A body of mass m is dropped from a height of h . Simultaneously anothe...
Text Solution
|
- solid sphere of radius r is gently placed on a rough horizontal ground...
Text Solution
|
- A solid ball of mass m and radius r spinning with angular velocity ome...
Text Solution
|
- A solid sphere with a velocity (of centre of mass) v and angular veloc...
Text Solution
|
- A solid sphere with angular velocity omega(0) is dropped on a rough su...
Text Solution
|
- A disc is given an angular velocity omega(0) and a linear velocity v(0...
Text Solution
|
- Statement-1 : In a perfectly inelastic collision between two spheres, ...
Text Solution
|
- A uniform solid sphere of mass m and radius r = 3m is projected along ...
Text Solution
|