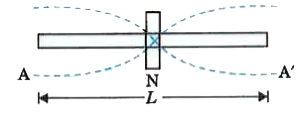
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-WAVES-CHAPTER PRACTICE TEST
- Determine the possible harmonics in the longitudinal vibrations of a r...
Text Solution
|
- What is the angle between the particle velocity and wave velocity in l...
Text Solution
|
- The density of nitrogen is 14 times than the density of hydrogen. What...
Text Solution
|
- What is the distance between two consecutive nodes and two consecutive...
Text Solution
|
- In an open organ pipe, second harmonic is 200 Hz. Find the frequency o...
Text Solution
|
- The fundamental frequency of an open organ pipe is 512 Hz. What will b...
Text Solution
|
- What is echo ? Why we cannot hear an echo in a small room ?
Text Solution
|
- On the basis of dimensional analysis, write the formula for speed of t...
Text Solution
|
- Show that the speed of sound is independent of the pressure.
Text Solution
|
- Distinguish between longitudinal waves and transverse waves.
Text Solution
|
- Bats have no eyes still they can travel during night. Why ?
Text Solution
|
- Show that the speed of sound increases by 61 cm/s for every degree ris...
Text Solution
|
- Calculate the ratio of length of an open organ pipe to closed organ pi...
Text Solution
|
- Write Newton's formula for speed of sound in air. What was the issue o...
Text Solution
|
- What do you mean by Doppler effect in sound ?
Text Solution
|