Topper's Solved these Questions
TRIANGLES
VK GLOBAL PUBLICATION|Exercise SELF ASSESSMENT TEST|10 VideosTRIANGLES
VK GLOBAL PUBLICATION|Exercise PROFICIENCY EXERCISE (SHORT ANSWER TYPE QUESTIONS-II)|39 VideosREAL NUMBERS
VK GLOBAL PUBLICATION|Exercise Self -Assessment Test|11 VideosVALUE-BASED QUESTIONS
VK GLOBAL PUBLICATION|Exercise Unit-VII : (Statistics & Probability)|8 Videos
Similar Questions
Explore conceptually related problems
VK GLOBAL PUBLICATION-TRIANGLES-PROFICIENCY EXERCISE (LONG ANSWER QUESTIONS)
- CD and GH are respectively the bisectors of /A C Band /E G Fsuch tha...
Text Solution
|
- In the Fig. given below, OB is the perpendicular bisector of the line ...
Text Solution
|
- In the adjoining figure, PQR, is a right triangle, right angled at Q. ...
Text Solution
|
- 14 In Fig. 6.21, PA, QB Rc and SD are all perpendiculars to a line l, ...
Text Solution
|
- If a perpendicular is drawn from the vertex containing the right angle...
Text Solution
|
- In given figure PQR is a right angled triangle, right angled at Q and ...
Text Solution
|
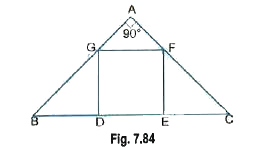
- In fig.7.84, DEFG is a square and angleBAC = 90°. Prove that: (i)...
Text Solution
|
- Prove that the area of the semicircle drawn on the hypotenuse of a rig...
Text Solution
|
- Ii DeltaPQR, PDbotQR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=...
Text Solution
|
- P and Q are the mid-points of the sides CA and CB respectively of a tr...
Text Solution
|
- In Fig. 7 .85, DEabs()BC and AD : DB = 5 : 4. Find ("Area"(DeltaDEF))/...
Text Solution
|
- D and E are points on the sides A B and A C respectively of a A...
Text Solution
|
- In Fig. 7.86, if D and E trisects BC. Prove that 8AE^(2) = 3AC^(2) + 5...
Text Solution
|
- In a triangle A B C ,\ A C > A B , D is the mid-point of B C and...
Text Solution
|
- In an equilateral triangle with side a , prove that Altitude =(a...
Text Solution
|