Topper's Solved these Questions
CIRCLES
VK GLOBAL PUBLICATION|Exercise SHORT ANSWER QUESTIONS - II (3 marks)|13 VideosCIRCLES
VK GLOBAL PUBLICATION|Exercise LONG ANSWER QUESTIONS (4 marks)|7 VideosCIRCLES
VK GLOBAL PUBLICATION|Exercise VERY SHORT ANSWER QUESTIONS (1 marks)|10 VideosARITHMETIC PROGRESSIONS
VK GLOBAL PUBLICATION|Exercise SELF ASSESSMENT TEST|10 VideosCOORDINATE GEOMETRY
VK GLOBAL PUBLICATION|Exercise SELF-ASSESSMENT TEST|10 Videos
Similar Questions
Explore conceptually related problems
VK GLOBAL PUBLICATION-CIRCLES -SHORT ANSWER QUESTIONS - I (2 marks)
- AB is a diameter of a circle and AC is its chord such that angleBAC=30...
Text Solution
|
- The length of tangent from an external point P on a circlewith centre ...
Text Solution
|
- If angle between two tangents drawn from a point P to a circle of radi...
Text Solution
|
- In the given figure, PA and PB are tangents to the circle from an exte...
Text Solution
|
- Prove that the line segment joining the points of contact of two paral...
Text Solution
|
- If from an external point P of a circle with centre O, two tangents PQ...
Text Solution
|
- In Fig common tangents AB and CD to two circles with centres O1 and O...
Text Solution
|
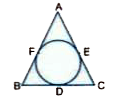
- The incircle of an isosceles triangle ABC, in which AB = AC, touches t...
Text Solution
|
- In Fig , XP and XQ are two tangents to the circle with centre O , draw...
Text Solution
|
- In the given figure, a circle inscribed in a triangle ABC, touches the...
Text Solution
|
- In Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with...
Text Solution
|
- In Fig AP and BP are tangents to a circle with centre O, such that AP ...
Text Solution
|
- From an external point P, two tangents PT and PS are drawn to a circle...
Text Solution
|
- In Fig , are two concentric circles of radii 6 cm and 4 cm with centre...
Text Solution
|