Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-WORK, ENERGY AND POWER-EXERCISES (ADDITIONAL EXERCISES)
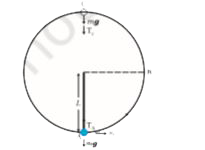
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- A bullet of mass 0.012kg and horizontal speed 70 ms^(-1) strikes a blo...
Text Solution
|
- Two inclined frictionless tracks, one gradual and the other steep meet...
Text Solution
|
- A 1 kg block situated on a rough incline is connected to a spring of s...
Text Solution
|
- A bolt of mass 0.3 kg falls from the ceiling of an elevator moving dow...
Text Solution
|
- A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a fr...
Text Solution
|
- Which of the following potential energy curves in Fig. 6. 18 cannot de...
Text Solution
|