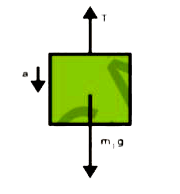
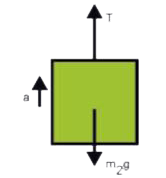
Text Solution
Verified by Experts
Topper's Solved these Questions
LAW OF MOTION
NCERT KANNAD|Exercise LET US IMPROVE OUR LEARNING (ALLPICATION OF CONEPTS )|5 VideosLAW OF MOTION
NCERT KANNAD|Exercise LET US IMPROVE OUR LEARNING (HIGHER ORDER THINKING QUESTIONS )|3 VideosIS MATTER PURE?
NCERT KANNAD|Exercise MULTIPLE CHOICE QUESTIONS|2 VideosMATTER AROUND US
NCERT KANNAD|Exercise Let us Improve our learning (Suggested project)|1 Videos
Similar Questions
Explore conceptually related problems
NCERT KANNAD-LAW OF MOTION -LET US IMPROVE OUR LEARNING (HIGHER ORDER THINKING QUESTIONS )
- Atwood machine Atwood used the system to prove Netwons laws of ...
Text Solution
|
- A vehicle has a mass of 1500 kg. What must be the force between the ve...
Text Solution
|
- Two ice skaters initially at rest, push of each other. If one skater w...
Text Solution
|
- Thre identical blocks, each of mass 10kg, are pulled as shown on the h...
Text Solution
|