Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
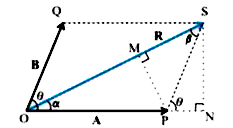
- Find the magnitude and direction of the resultant of two vectors A and...
Text Solution
|
- Two vectors having equal magnitudes A make an angle theta with eahc ot...
Text Solution
|
- Find the magnitude and direction of the resultant of two vectors A and...
Text Solution
|
- Find the magnitude and direction of the resultant of two vectors A and...
Text Solution
|
- चित्र में दिखाये गये दो सदिशों vecA और vecB के बीच का कोण theta है। इन...
Text Solution
|
- चित्र में दिखाए गए दो सदिशों A तथा B के बीच का कोण theta है। इनके पर...
Text Solution
|
- Find the magnitude and direction of the resultant of two vectors A and...
Text Solution
|
- Find the magnitude and direction of the resultant of two vectors A and...
Text Solution
|
- Find the magnitude and direction of the resultant of two vectors A and...
Text Solution
|