Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
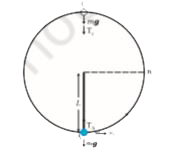
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- A bob of mass m suspended by a light string of length L is whirled int...
Text Solution
|
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|