Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
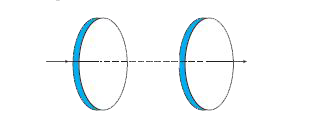
- Figure 8.6 shows a capacitor made of two circular plates each of radiu...
Text Solution
|
- Figure shows a capacitor made of two circular plates each of radius 12...
Text Solution
|
- A parallel plate capacitor made of two circular plates each of radius ...
Text Solution
|
- Fig. shows a capacitor made of two circular plates each of radius 12 c...
Text Solution
|
- The figure shows a capacitor made of two circular plates each of radiu...
Text Solution
|
- A capacitor is made of two circular plates each of radius 12 cm, and s...
Text Solution
|
- Figure shows a capacitor made of two circular plates each of radius 12...
Text Solution
|
- Figure 8.6 shows a capacitor made of two circular plates each of radiu...
Text Solution
|
- Figure 8.6 shows a capacitor made of two circular plates each of radiu...
Text Solution
|