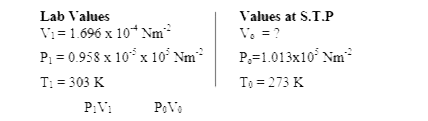Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the determination of molecular mass by Victor - Meyer's Method 0.79...
Text Solution
|
- The vapour pressure of benzene is 1.53 xx 10^(4) Nm^(-2) at 303 K and ...
Text Solution
|
- 10g of cane sugar (molecular mass = 342) in 1 xx 10^(-3) m^(3) of solu...
Text Solution
|
- Calculate the mass and density of the earth. Given that Gravitational ...
Text Solution
|
- An ideal gas expands from the volume of 1xx10^(-3) m^(3) " to "1xx10^(...
Text Solution
|
- In the Victor Meyer's method for the determination of molecular mass o...
Text Solution
|
- In the determination of molecular mass by Victor - Meyer's Method 0.79...
Text Solution
|
- In the determination of molecular mass by Victor - Meyer's Method 0.79...
Text Solution
|
- In the determination of molecular mass by Victor - Meyer's Method 0.79...
Text Solution
|