Similar Questions
Explore conceptually related problems
Recommended Questions
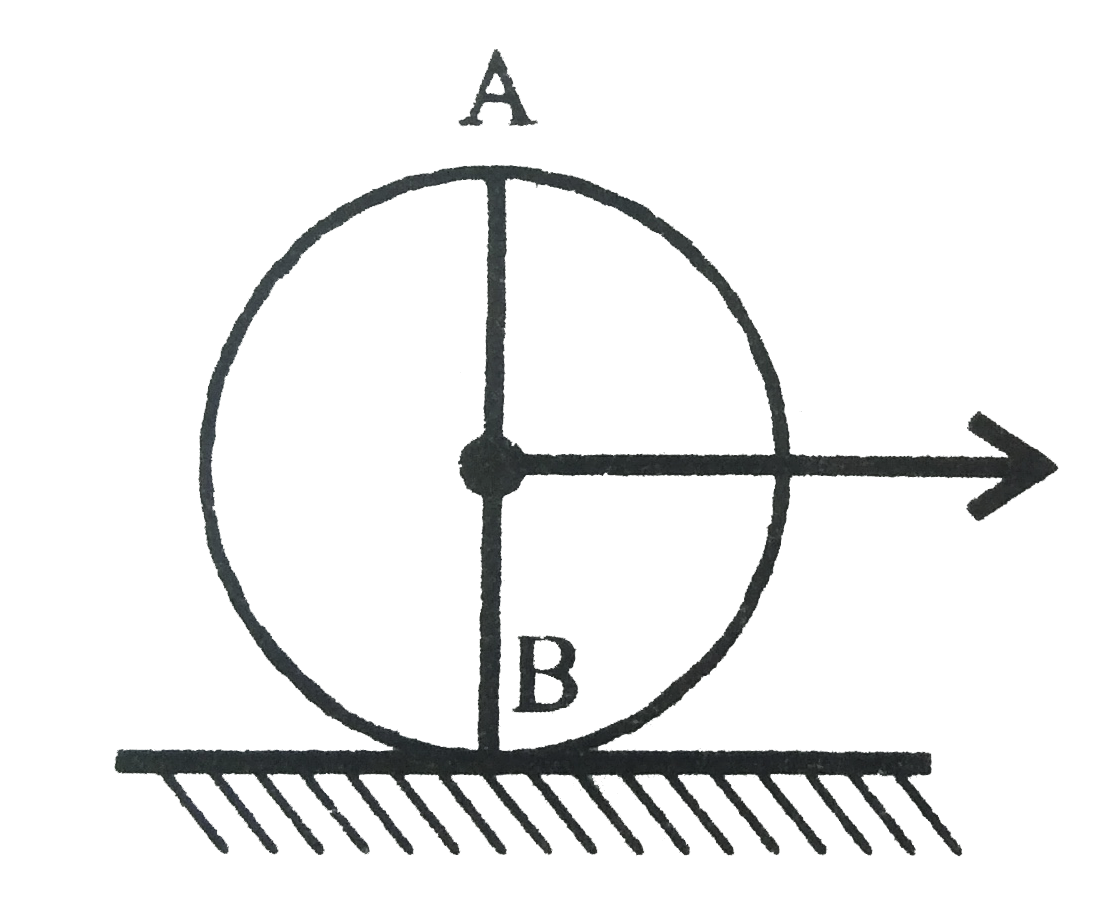
- A uniform disc is rolling on a horizontal surface. At a certain instan...
Text Solution
|
- A circular disc of radius r is rolling without slipping on a horizonta...
Text Solution
|
- A uniform disc is rolling on a horizontal surface. At a certain instan...
Text Solution
|
- A disc of mass m and radius r placed on a routh horizontal surface. A ...
Text Solution
|
- A disc of radius r = 0.1 m is rolled from a point A on a track as show...
Text Solution
|
- The radius of gyration of a uniform disc of radius R, about an axis pa...
Text Solution
|
- A disc of mass M and radius R rolls on a horizontal surface and then r...
Text Solution
|
- A disc of mass M and radius R rolls on a horizontal surface and then r...
Text Solution
|
- A circular disc of radius R rolls without slipping along the horizonta...
Text Solution
|
 .
.