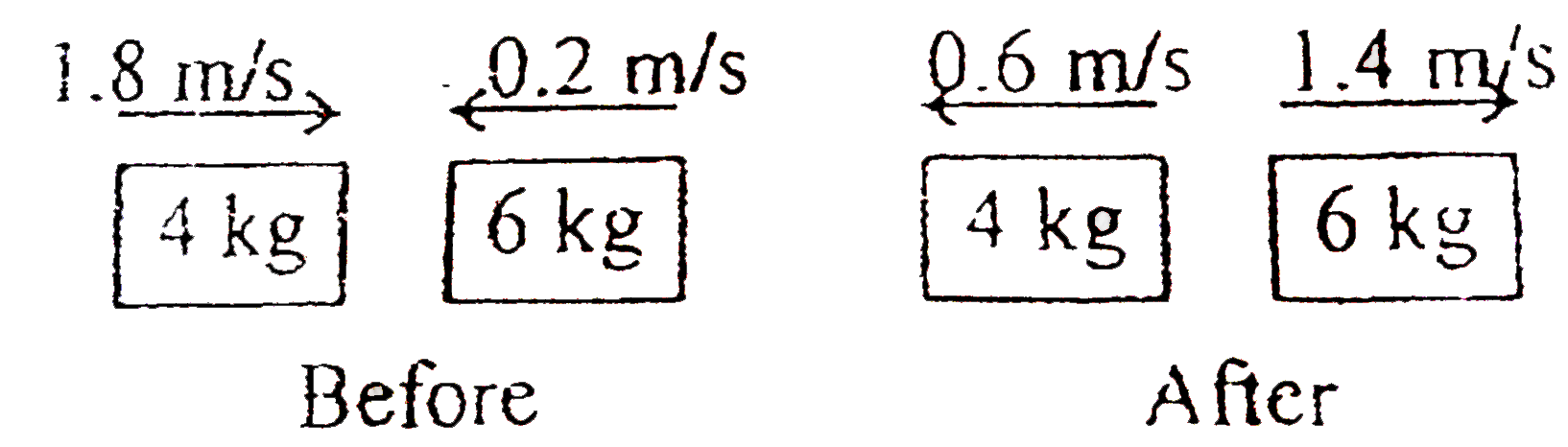Similar Questions
Explore conceptually related problems
Recommended Questions
- In figure, determine the character of the collision. The masses of the...
Text Solution
|
- In figure, determine the character of the collision. The masses of the...
Text Solution
|
- Find the final velocities of the masses after in collision the given s...
Text Solution
|
- In a one-dimensional collision between two particles, their relative v...
Text Solution
|
- The ratio of relative velocity of separation after collision to the re...
Text Solution
|
- Derive velocities after the collision in terms of velocities before co...
Text Solution
|
- Obtain the expression for the velocities of the two bodies after colli...
Text Solution
|
- 2m द्रव्यमान वाला एक गुटका जो अचर वेग 3vecv से चल रहा है, एक अन्य गुटक...
Text Solution
|
- In one-dimensional elastic collision, the relative velocity of approac...
Text Solution
|