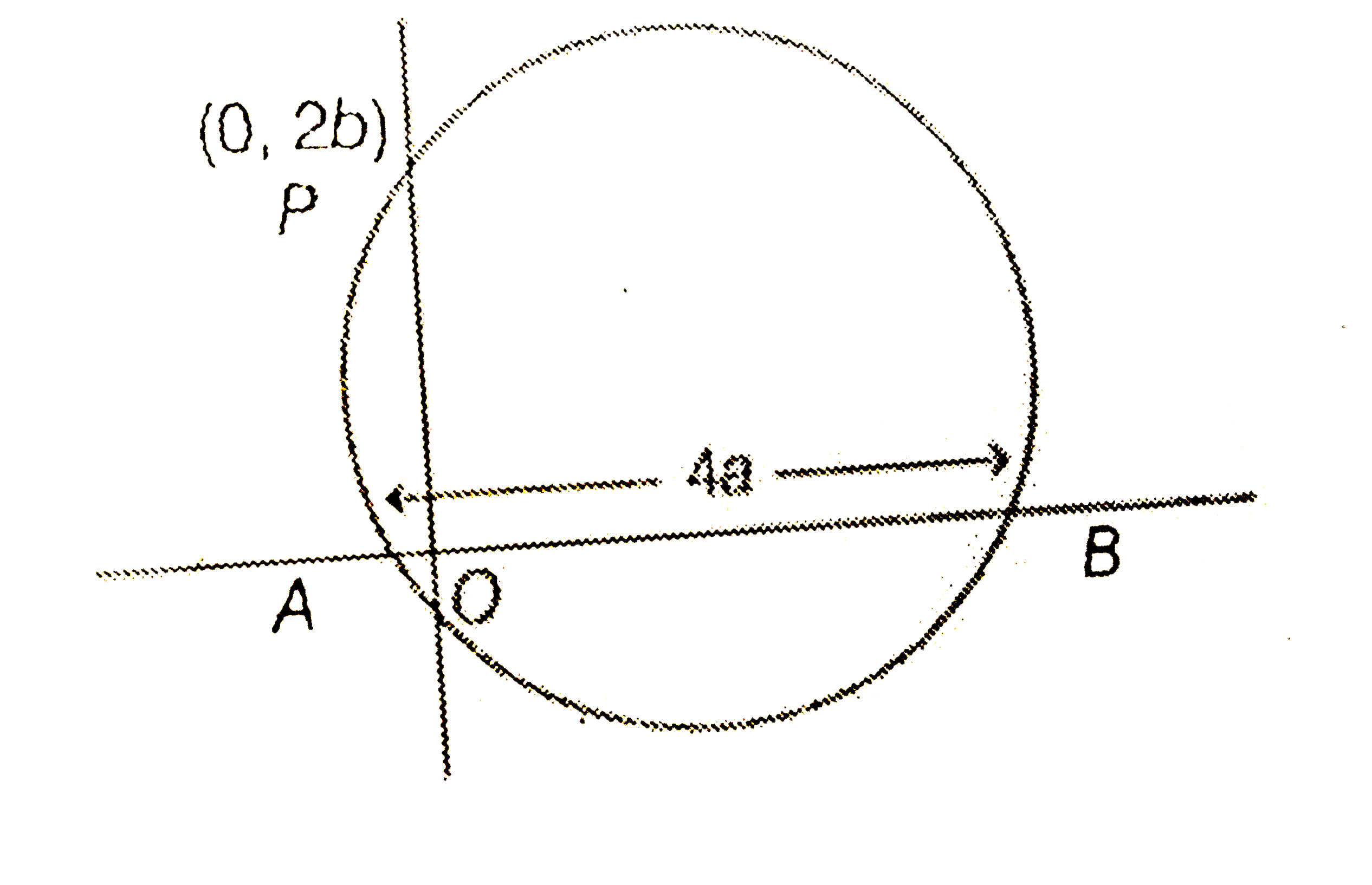
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PARABOLA
IIT JEE PREVIOUS YEAR|Exercise TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (ASSERTION AND REASON )|1 VideosPARABOLA
IIT JEE PREVIOUS YEAR|Exercise TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (INTERGER )|2 VideosMISCELLANEOUS
IIT JEE PREVIOUS YEAR|Exercise MISCELLANEOUS|87 VideosPERMUTATIONS AND COMBINATIONS
IIT JEE PREVIOUS YEAR|Exercise Dearrangement and Number of Divisors (Fill in the Blank )|1 Videos
Similar Questions
Explore conceptually related problems
IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ANALYTICAL & DESCRIPTIVE )
- A circle cuts the chord on x-axis of length 4a. If this circle cuts th...
Text Solution
|
- The angle between a pair of tangents drawn from a point P to the hyper...
Text Solution
|
- From a pt A common tangents are drawn to a circle x^2 +y^2 = a^2/2 and...
Text Solution
|
- Points A, B, C lie on the parabola y^2=4ax The tangents to the parabol...
Text Solution
|
- Show that the locus of a point that divides a chord of slope 2 of the ...
Text Solution
|
- Through the vertex 'O' of parabola y^2=4x, chords OP and OQ are drawn...
Text Solution
|