Home
Class 12
MATHS
Tangent and normal are drawn at P(16,16)...

Tangent and normal are drawn at P(16,16) on the parabola `y^2=16x` which intersect the axis of the parabola at A and B respectively. If C is the centre of the circle through the points P,A and B and `angle CPB=theta` then the value of `tan theta` is

A

`(1)/(2)`

B

2

C

3

D

`(4)/(3)`

Text Solution

Verified by Experts

The correct Answer is:
B
Equation of tangent and normal to the curve `y^(2) = 16x` at (16, 16) is `x- 2y + 16 = 0` and `2x + y - 48 = 0` respectively.

`A = (-16, 0) B = (24, 0)`
`:' C` is the centre of circle passing through PAB i.e.,
Slope of `PC = (16 - 0)/(16 - 4) = (16)/(12) = (4)/(3) = m_(1)`
Slope of `PB = (16 - 0)/(16 - 24) = (16)/(-8) = - m_(2)`
`tan theta = |(m_(1) - m_(2))/(1 + m_(1)m_(2))|`
`implies tan theta = |((4)/(3) + 2)/(1 - ((4)/(3))(2))| implies tan theta = 2`
Promotional Banner

Topper's Solved these Questions

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 2 EQUATION OF TANGENTS AND PROPERTIES (ASSERTION AND REASON )|1 Videos

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 2 EQUATION OF TANGENTS AND PROPERTIES OBJECTIVES QUESTIONS II (ONE OR MORE THAN CORRECT OPTION )|1 Videos

  • PARABOLA

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (INTERGER )|2 Videos

  • MISCELLANEOUS

    IIT JEE PREVIOUS YEAR|Exercise MISCELLANEOUS|87 Videos

  • PERMUTATIONS AND COMBINATIONS

    IIT JEE PREVIOUS YEAR|Exercise Dearrangement and Number of Divisors (Fill in the Blank )|1 Videos

Similar Questions

Explore conceptually related problems

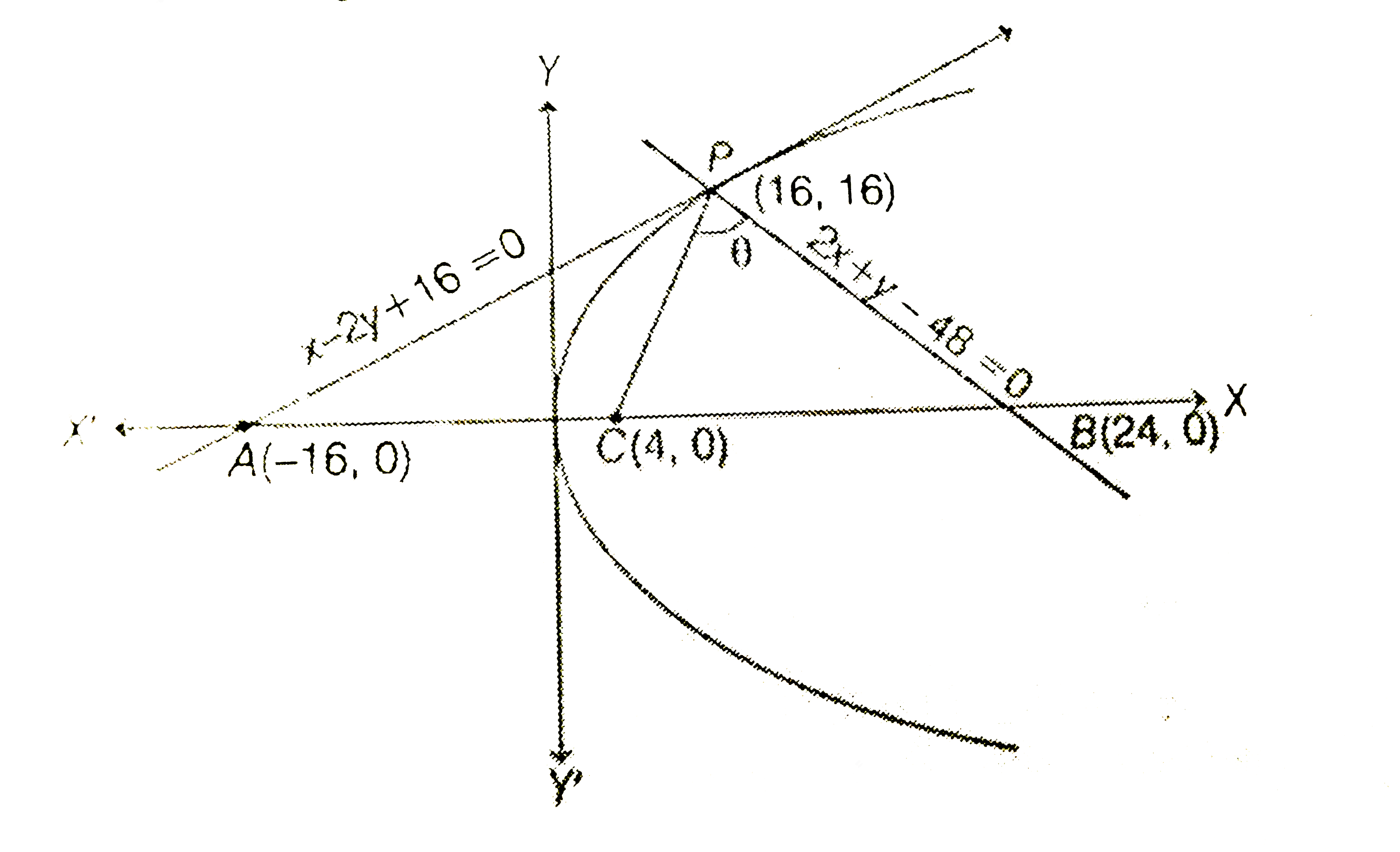
Tangent and normal are drawn at the point P-=(16 ,16) of the parabola y^2=16 x which cut the axis of the parabola at the points Aa n dB , rerspectively. If the center of the circle through P ,A ,a n dB is C , then the angle between P C and the axis of x is (a)tan^(-1)(1/2) (b) tan^(-1)2 (c)tan^(-1)(3/4) (d) tan^(-1)(4/3)

A tangent and a normal are drawn at the point P(8, 8) on the parabola y^(2)=8x which cuts the axis of the parabola at the points A and B respectively. If the centre of the circle through P, A and B is C, then the sum f sin(anglePCB) and cot(anglePCB) is equal to

The tangent and normal at the point p(18, 12) of the parabola y^(2)=8x intersects the x-axis at the point A and B respectively. The equation of the circle through P, A and B is given by

The tangent and normal at the point P(4,4) to the parabola, y^(2) = 4x intersect the x-axis at the points Q and R, respectively. Then the circumcentre of the DeltaPQR is

For the parabola y^(2)=8x tangent and normal are drawn at P(2.4) which meet the axis of the parabola in A and B .Then the length of the diameter of the circle through A,P,B is

A tangent and a normal are drawn at the point P(2,-4) on the parabola y^(2)=8x , which meet the directrix of the parabola at the points A and B respectively. If Q (a,b) is a point such that AQBP is a square , then 2a+b is equal to :

Normals are drawn at points P, Q are R lying on the parabola y^(2)=4x which intersect at (3, 0), then

Normals are drawn at points A,B, and C on the parabola y^(2)=4x which intersect at P.The locus of the point P if the slope of the line jocuing the feet of two of them is 2, is