Similar Questions
Explore conceptually related problems
Recommended Questions
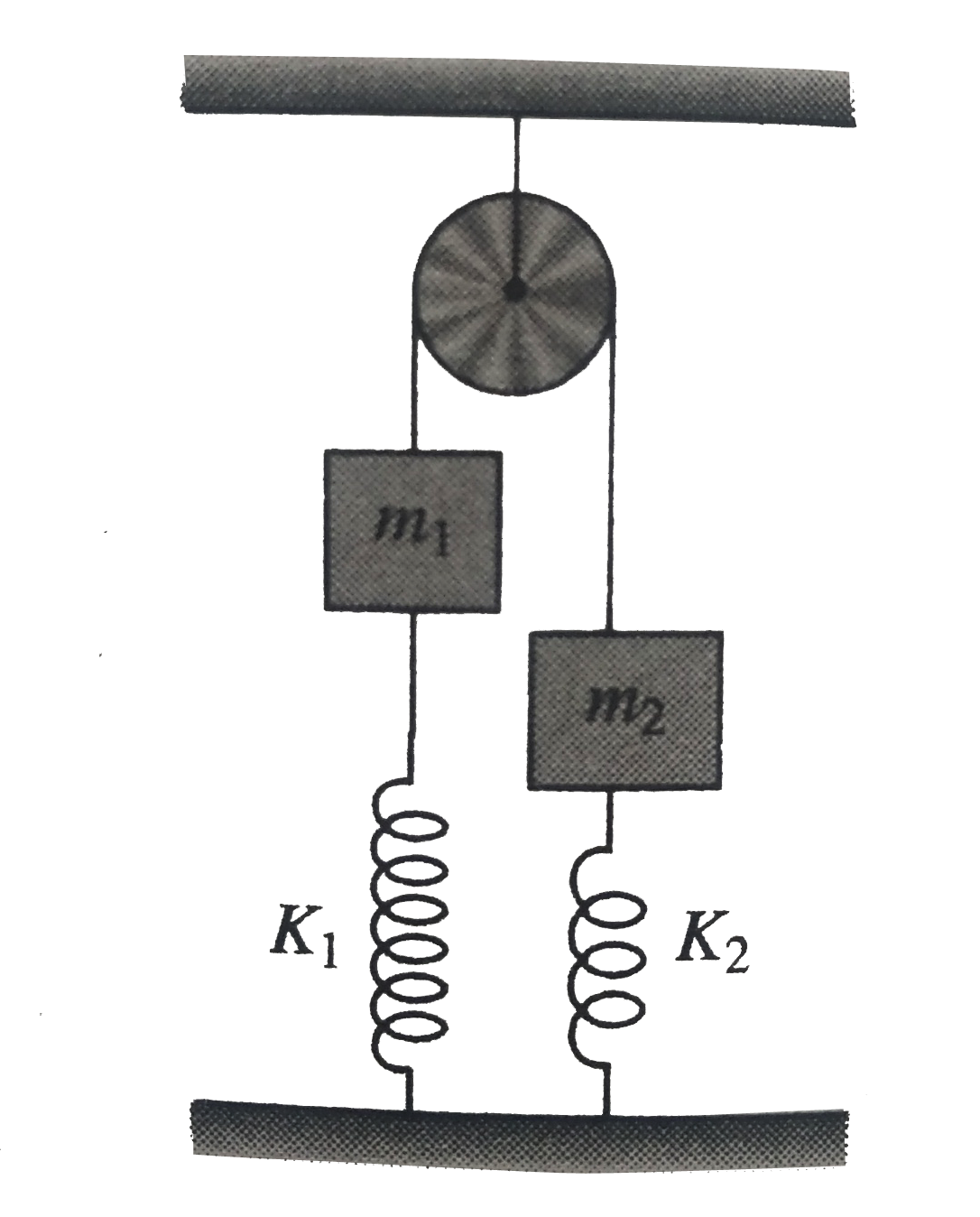
- The system shown in fig is in equilibrium . Masses m(1) and m(2) are 2...
Text Solution
|
- The masses in figure slide on a frictionless table. m(1) but not m(2),...
Text Solution
|
- The system shown in fig is in equilibrium . Masses m(1) and m(2) are 2...
Text Solution
|
- Two masses m(1) and m(2) are attached to a spring balance S as shown i...
Text Solution
|
- Two masses m(1)and m(2) are suspended from a spring of spring constant...
Text Solution
|
- Two blocks of masses m(1) and m(2) are kept on a smooth horizontal tab...
Text Solution
|
- The two masses m(1) and m(2) are joined by a spring as shown. The syst...
Text Solution
|
- Spring of spring constant k is attached with a block of mass m(1) , as...
Text Solution
|
- The system shown in the figure is in equilibrium. Masses m(1) & m(2) a...
Text Solution
|