Similar Questions
Explore conceptually related problems
Recommended Questions
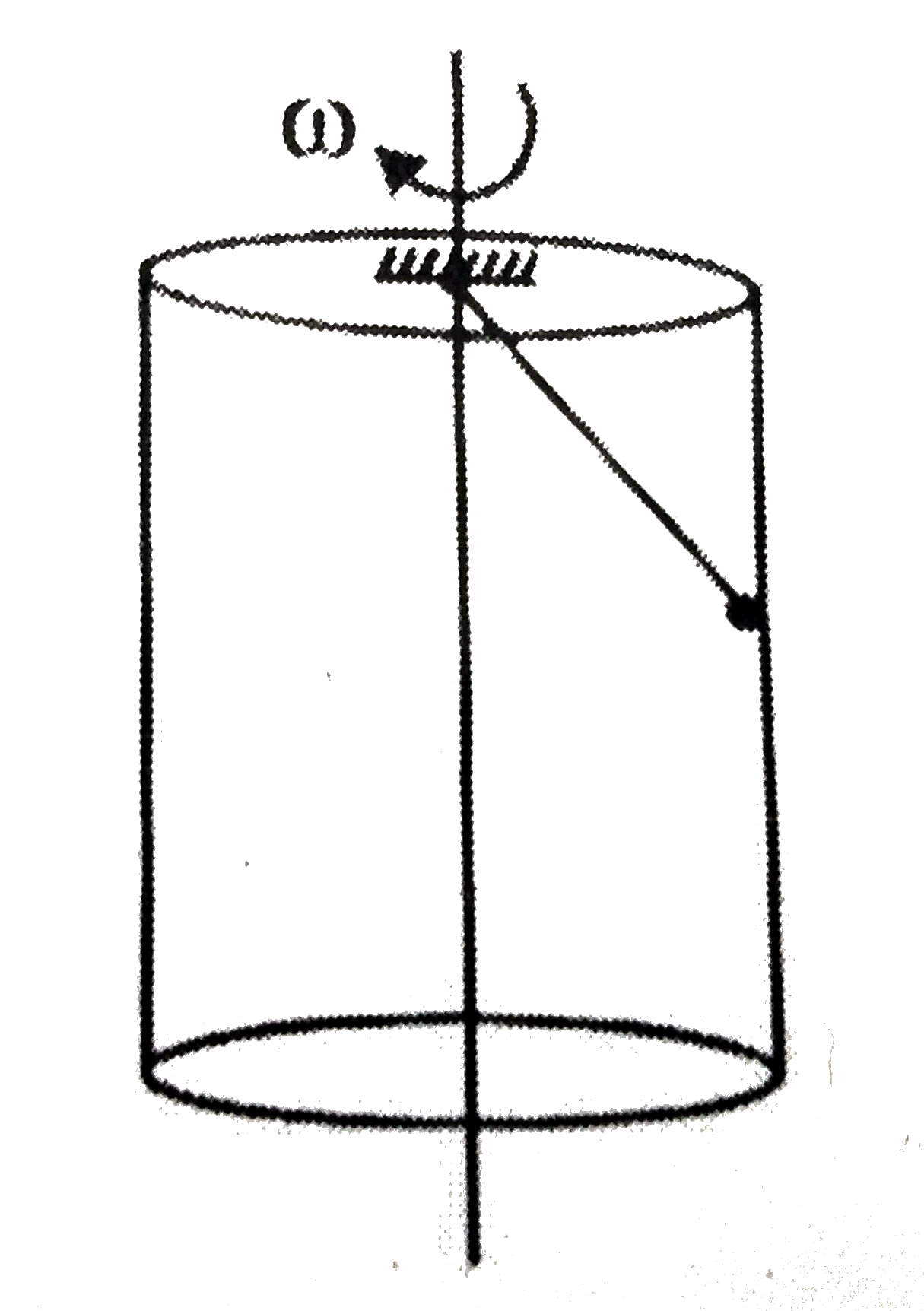
- In the shown figure inside a fixed hollow cylinder with vetical axis a...
Text Solution
|
- An cylinder of mass m is rotated about its axis by an angular velocity...
Text Solution
|
- A hollow cylinder of radius R rotates about its axis which is vertical...
Text Solution
|
- The axis of the uniform cylinder in figure is fixed. The cylinder is i...
Text Solution
|
- The axis of the uniform cylinder in figure is fixed. The cylinder is i...
Text Solution
|
- In the shown figure inside a fixed hollow cylinder with vetical axis a...
Text Solution
|
- A solid cylinder of mass 20 kg rotates about its axis with angular vel...
Text Solution
|
- Show that the square of the radius of gyration of a hollow cylinder is...
Text Solution
|
- What is the radius of gyration for a (a) hollow cylinder (b) solid cyl...
Text Solution
|