Home
Class 12
MATHS
A particle moves along x-axis in such a ...

A particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= `(8-4t + 6t^(2)`) metre. The velocity of the particle will vary with time according to the graph

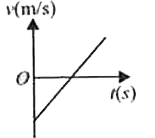
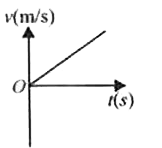
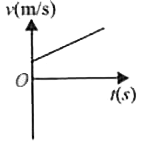
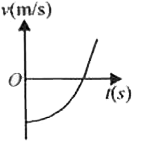
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • APPLICATION OF DERIVATIVES

    MTG-WBJEE|Exercise WB JEE WORKOUT ( CATEGORY 2 : Single Option Correct Type (2 Marks) )|15 Videos

  • APPLICATION OF DERIVATIVES

    MTG-WBJEE|Exercise WB JEE WORKOUT ( CATEGORY3 : One or More than One Option Correct Type (2 Marks)|15 Videos

  • A.P.,G.P.,H.P.

    MTG-WBJEE|Exercise WB JEE Previous Years Questions ( CATEGORY 2 : Single Option Correct Type (2 Mark ) )|5 Videos

  • APPLICATION OF INTEGRALS

    MTG-WBJEE|Exercise WE JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)|3 Videos

Similar Questions

Explore conceptually related problems

A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x = (2-5t +6t^(2))m . The initial velocity of the particle is

A particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4-2t+t^(2) . The speed of the particle will vary with time as

A particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x = A_0 - A_1 t + A_2 t^2 . The initial velocity of the particle is.

A particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x = 2 – 5t + 6t^(2) . The initial velocity and acceleration of particle will respectively be-

A particle moves along the x-axis such that its co-ordinate (x) varies with time (t), according to the expression x=2 -5t +6t^(2), where x is in metres and t is in seconds. The initial velocity of the particle is :–

A particle moves in an XY-plane in such a way that its x and y-coordinates vary with time according to x(t)=t^(3)-32t, y(t)=5t^(2)+12 Find the acceleration of the particle, if t = 3 s.

A particle moves a distance x in time t according to equation x^(2) = 1 + t^(2) . The acceleration of the particle is

A particle moves in the x-y plane. It x and y coordinates vary with time t according to equations x=t^(2)+2t and y=2t . Possible shape of path followed by the particle is

The acceleration of a'particle starting from rest, varies with time according to the relation a=kt+c . The velocity of the particle after time t will be :

The acceleration of a particle which starts from rest varies with time according to relation a=2t+3. The velocity of the particle at time t would be