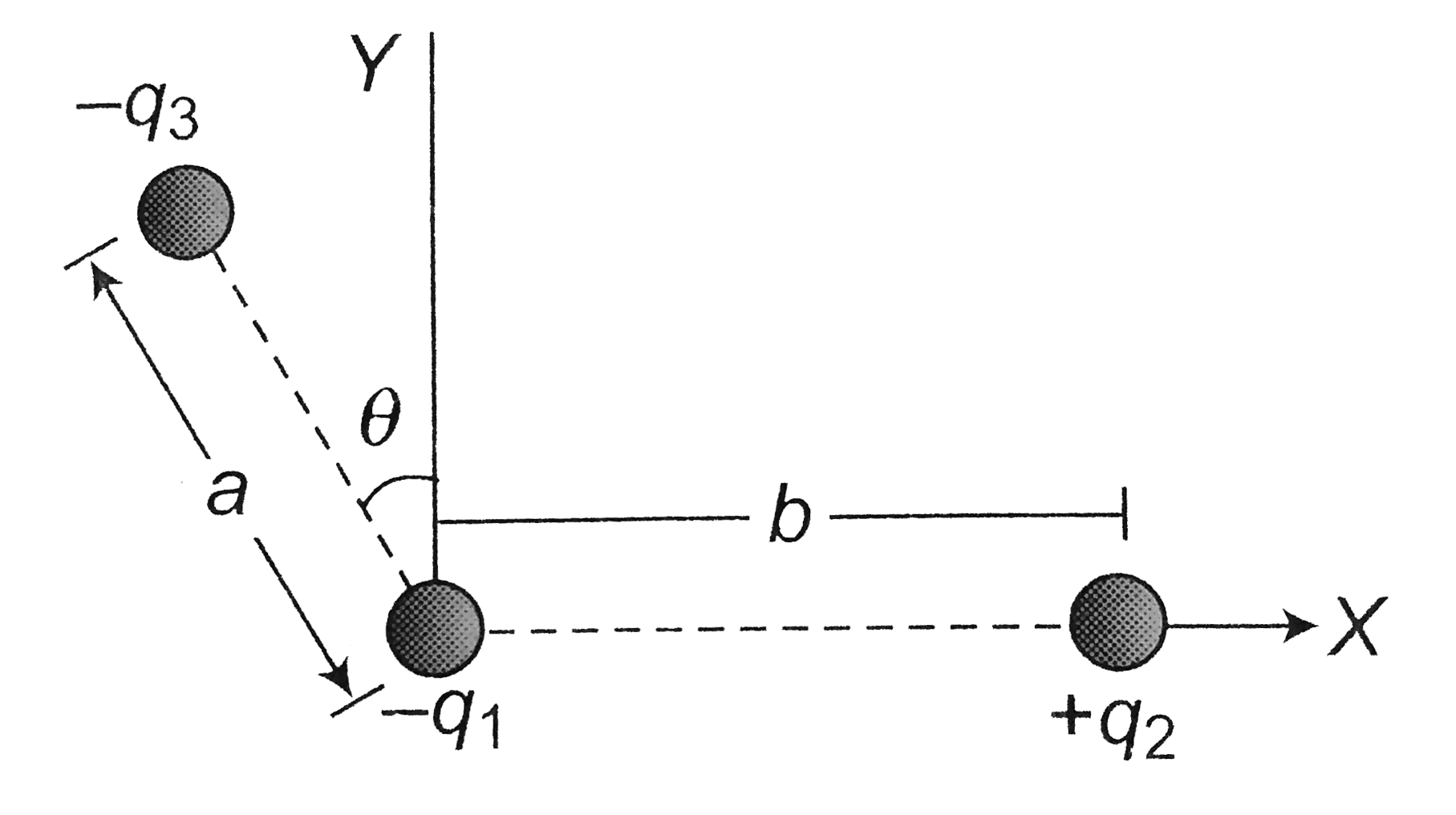
Three charges `-q_(1), +q_(2)` and `-q_(3)` are placed as shown in the figure. The `x`-component of the force on `-q_(1)` is proportional to

Three charges q_(1), q_(2) and q_(3) are shown in figure . Determine the net force acting on charge q_(1) . The charges and separation are given as q_(1) =- 1.0 xx 10^(-6)C, q_(2) =+ 3.0 xx 10^(-6)C , and q_(3) = - 2.0 xx 10^(-6)C, r_(12) = 15 cm, r_(13) = 10 cm and theta = 30^(@) .

The value of charge q_1 ,q_2 and q_3 as shown in the figure are

Assertion: Two charges q_(1) and q_(2) are placed at separation r . Then magnitude of the force on each charge is F . Reason: Now a third charge q_(3) is placed near q_(1) and q_(2) . Then force on q_(1) and q_(2) remains F .

Two points charge q_(1) and q_(2)(=q_(1)//2) are placed at points A(0,1) and B(1,0) as shown in the figure.The electric field vector at point P(1,1) makes an angle q with the x-axis ,then the angle q is

Assertion: Four point charges q_(1),q_(2),q_(3) and q_(4) are as shown in Fig,The flux over the shown Gaussians surface depends only on charges q_(1) and q_(2) Reason:Electric field at all points on Gaussians surface depends on any charges q_(1) and q_(2)

Three charges q_(1) = 1 mu C, q_(2) = -2 muC and q_(3) = 3mu C are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge q_(1) . How to proceed Charge q_(2) will attract charge q_(1) (along the line joining them) and charge q_(3) will repel charge q_(1) . Therefore, two forces will act on q_(1) , one due to q_(2) and another due to q_(3) . Since , the force is a vector quantity both of these force (say F_(1) and F_(2) ) will be added by vector method. Following are two methods of their addition

Three charges q_(1) = 1 mu C, q_(2) = -2 muC and q_(3) = 3mu C are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge q_(1) . How to proceed Charge q_(2) will attract charge q_(1) (along the line joining them) and charge q_(3) will repel charge q_(1) . Therefore, two forces will act on q_(1) , one due to q_(2) and another due to q_(3) . Since , the force is a vector quantity both of these force (say F_(1) and F_(2) ) will be added by vector method. Following are two methods of their addition