Home
Class 9
PHYSICS
Atwood machine Atwood used the sy...

Atwood machine

Atwood used the system to prove Netwons laws of motion. Atowood machine consists of two loads of mases `m _(1) and m _(2)` attached to the ends of a limp of inextensible string as shown in tghe figure 11. The string runs over a pully. FInd the acceleration of each load and tension in the string `(m _(1) gt m _(2))`

Text Solution

Verified by Experts

we know that tension of string always tries to pull te bodies up.

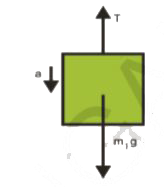
From the FBD of the mass `m _(1),` there exist two forces on the load of mass `m _(1),` one is tension of the string acting in upward direction and weight of the load `(m_(1) g)` acting in downward direction.
The net force on `m _(1) F _(n et) = m_(1) a`
`implies m _(1) g -T =m_(1) a ---------------(1)`
Thus the net force `(F_(n et))` acting on mass `m _(1)` produces an acceleration .a. in it.
When `m _(1)` moves down, `m _(2)` moves up. So the magnitudes of acceleration are same.

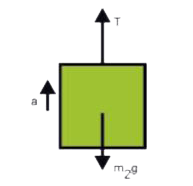
From the FBD of mass `m _(2)`
`F _(n et) =T - m _(2) g =m_(2)a ----------------(2)`
Solving (1) and (2) equations, we get
`a = ((m _(1) - m _(2) g)/( m _(1) + m _(2))`
` T = ( 2m _(1) m _(2) g)/( m _(1) +m_(2))`
Promotional Banner

Topper's Solved these Questions

  • LAW OF MOTION

    NCERT TAMIL|Exercise THINK AND DISCUSS|12 Videos

  • LAW OF MOTION

    NCERT TAMIL|Exercise LET US IMPROVE OUR LEARNING (REFLECTIONS ON CONCEPTS )|3 Videos

  • IS MATTER PURE?

    NCERT TAMIL|Exercise THINK AND DISCUSS|9 Videos

  • LIGHT

    NCERT TAMIL|Exercise Problem |5 Videos

Similar Questions

Explore conceptually related problems

Three blocks of masses m_1, m_2 and m_3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m_1

If the tension in the string in the figure. Is 16 N and the acceleration of each block is 0.5 m/s^2 , find the friction coefficients at the two contacts with h blocks.

A constant force F=m_2g/s is applied on the block of mass m_1 as shown in figure. The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m_1

A light rod of length has two masses m_1 and m_2 attached to its two ends.The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is

Calculate the tension in the string shown in figure. The pulley and the string are light and all surfaces are frictionless. Take g=10 m/ s^2 .

If two masses m_1 and m_2 (m_1 gt m_2) tied to string moving over a frictionless pulley, then acceleration of masses

Two blocks of masses m_1 and m_2 (m_1 gt m_2) in contact with each other on frictionless, horizontal surface. If a horizontal force F is given on m_1 set into motion with acceleration a, then reaction force on mass m_1 by m_2 is

Two masses m_1 = 5 kg and m_2 = 4 kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of each mass when left free to move? (g =9.8ms^(2))