A rectangle glass wedge (prism) is immersed in water as shown in figure E-a. For what value of angle `alpha`, will the beam of light, which is normally incident on AB, reach AC entirely as shown in figure E-b. Take the refractive index of water as `4/3` and the refractive index of glass as `3/2`.

Explanation

From the geometry of figure E-b it is clear that, the angle of incidence on the side BC is equal to `alpha` (dotted line is a normal drawn at the point of incidence). The ray should undergo total internal reflection to reach AC. For occurrence of total internal reflection, the value of `alpha` must be greater than the critical angle at interface of water and glass.
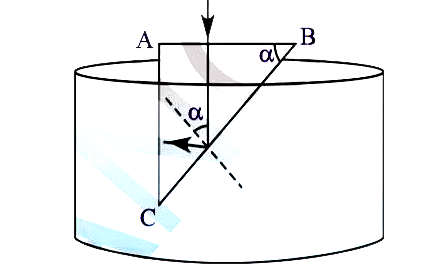
Let .C. be the critical angle of interface of glass and water. From the given condition `alpha gt C .......(1)`
We know, `sin C=1/(n^(12))` ........(2)
`n_(12)=3/2 / 4/3=9/8`
From equation 2, we get
`sin C=8/9 rArr C=62^(@)30^(1)`
Hence `alpha` is greater than `C=62^(@)30^(1)`
Let us see few activities of total internal reflection.