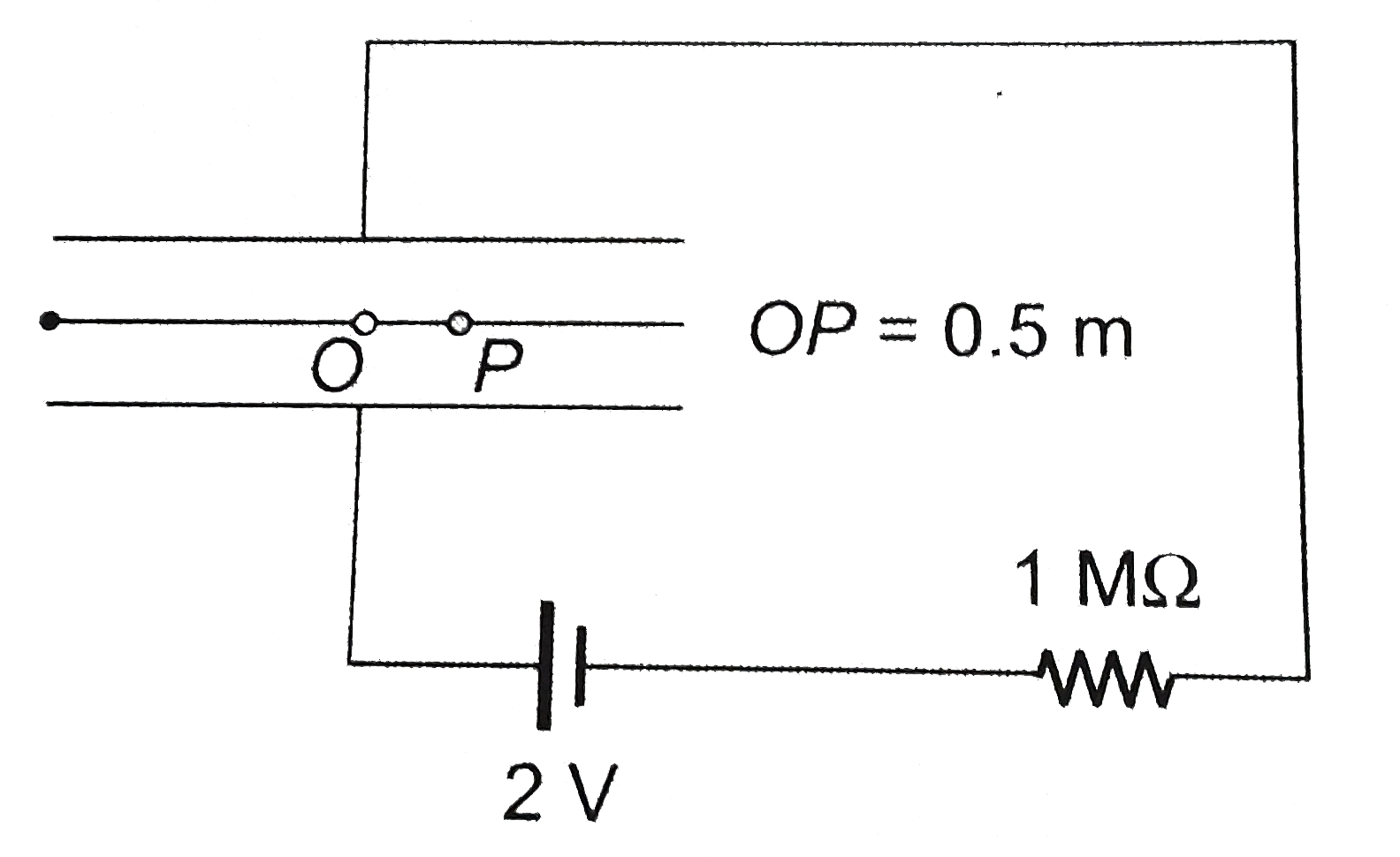
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A parallel plate capacitor with circular plates of radius 1m has a cap...
Text Solution
|
- A parallel plate capacitor with circular plates of radius 1m has a cap...
Text Solution
|
- A parallel plate capacitor is charged by connecting is plates to the t...
Text Solution
|
- A parallel plate capacitor with circular plates of radius 1m has a cap...
Text Solution
|
- A parallel plate capacitor with circular plates of radius 1m has a c a...
Text Solution
|
- एक समांतर प्लेट संधारित्र जिसकी व्रत्ताकार प्लेटों की त्रिज्या 1m है ध...
Text Solution
|
- किसी समांतर प्लेट संधारित्र की वृत्ताकार प्लेटो की त्रिज्या 1 m तथा धा...
Text Solution
|
- A parallel plate capacitor with circular plates of radius 1m has a cap...
Text Solution
|
- एक समांतर प्लेट संधारित्र जिसकी वृताकार प्लटो की त्रिज्या 1m ...
Text Solution
|