Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
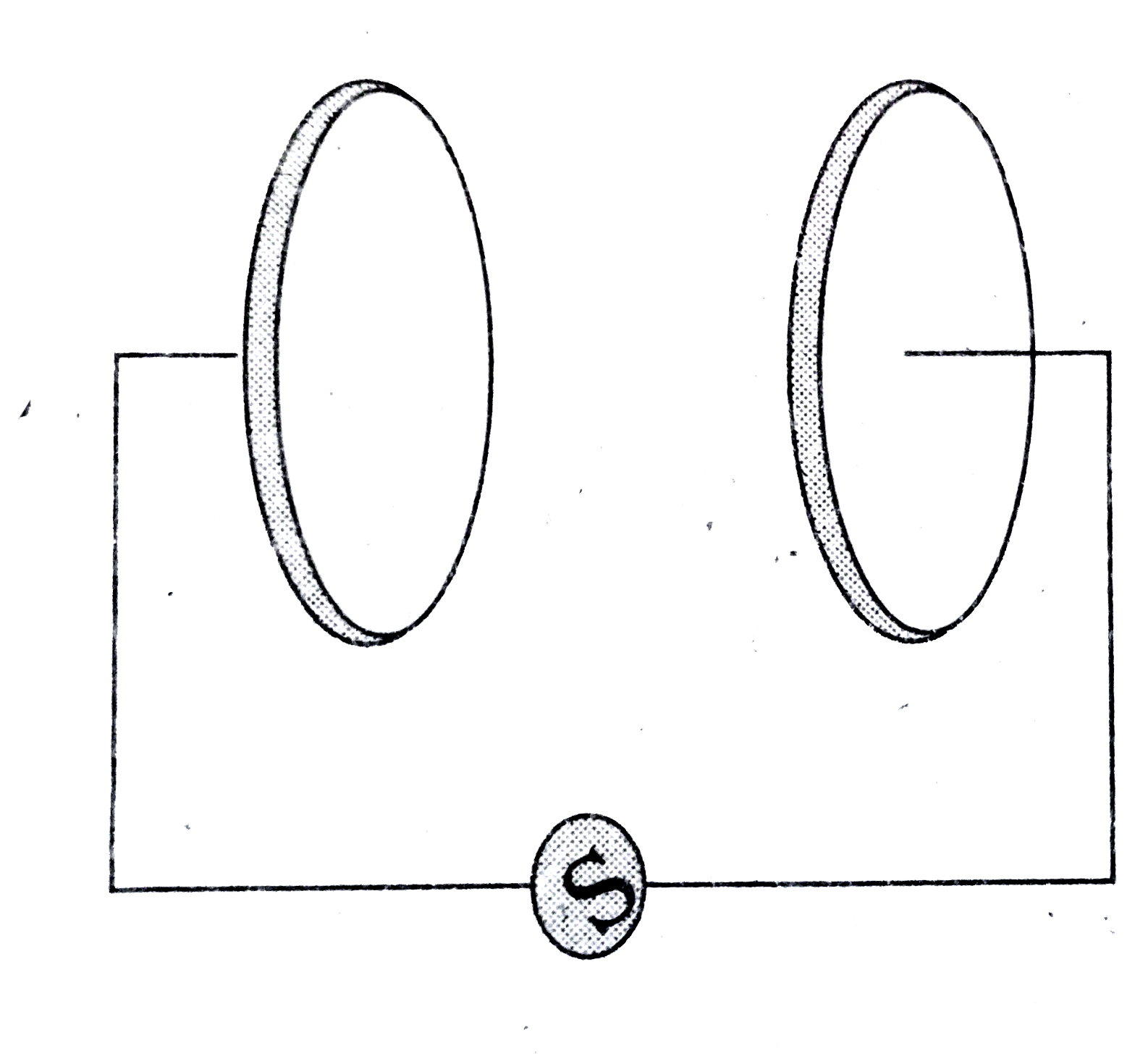
- A parallel plate capacitor in the figure made of circular plates each ...
Text Solution
|
- A parallel plate capacitor in the figure made of circular plates each ...
Text Solution
|
- A parallel plate capacitor in the figure made of circular plates each ...
Text Solution
|
- A parallel plate capacitor in the figure made of circular plates each ...
Text Solution
|
- एक समांतर प्लेट संधरित्र R = 6 .0 सेमी त्रिज्या की दो वृताकार...
Text Solution
|
- एक समांतर प्लेट संधरित्र R = 6 .0 सेमी त्रिज्या की दो वृताकार...
Text Solution
|
- A parallel plate capacitor (figure) made of circular plates each of ra...
Text Solution
|
- A parallel plate capacitor (Fig. 8.7) made of circular plates each of ...
Text Solution
|
- A parallel plate capacitor (Fig. 8.7) made of circular plates each of ...
Text Solution
|