The angular velocity , `omega` of a rotating body or shaft can be measured by attaching an open cylinder of liquid , as shown in Fig and measuring the change in the fluid level , `H- h_(0)` , caused by the rotation of the fluid . Determine the relationship between this change in fluid level and the angular velocity . Assume no fluid is spilling out of the vessel.

Explanation

The height h , of the free surface above the tank bottom can be determined as follows
`h - (omega^(2) r^(2))/(2 g) + h_(0)`

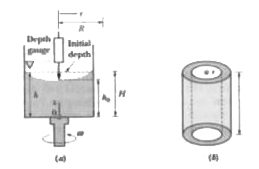
The initial volume of fluid in the tank , `V_(i) = pi R^(2) H`
The volume of the fluid with the rotating tank can be found by considering a differential element of cylindrical shape as shown in Fig . This cylindrical shell is taken at some arbitary radius , r and thickness dr . Thus , its volume is
`dV = 2 pi r h dr`
The total volume is , therefore ,
`V. = 2 pi int_(0)^(R) r ((omega^(2) r^(2))/(2 g) + h_(0)) dr = (pi omega^(2) R^(4))/( 4 g) + pi R^(2) h_(0)`
Since the volume of the fluid in the tank must remain constant (given that none spills over the top) , it follows that `pi R^(2) H = (pi omega^(2) R^(4))/(4 g) = pi R^(2) h_(0)`
or `H - h_(0) = (omega^(2) R^(2))/(4 g)`