A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CHEMICAL EQUILIBRIUM
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE -I) LEVEL-II (MATRIX MATCHING TYPE QUESTIONS )|5 VideosCHEMICAL EQUILIBRIUM
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE -II) (LEVEL - I) STRAIGHT OBJECTIVE TYPE QUESTIONS|17 VideosCHEMICAL EQUILIBRIUM
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE -I) LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QESTIONS )|20 VideosCARBOXYLIC ACIDS AND DERIVATIVES
AAKASH SERIES|Exercise CONVERSIONS|19 VideosCHEMICAL KINETCS
AAKASH SERIES|Exercise EXERCISE - 3.2|45 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-CHEMICAL EQUILIBRIUM-PRACTICE SHEET (EXERCISE -I) LEVEL-II (LINKED COMPREHENSION TYPE QUESTIONS )
- As per lechatelier's principle any equilibrium state nullifies the eff...
Text Solution
|
- As per lechatelier's principle any equilibrium state nullifies the eff...
Text Solution
|
- As per lechatelier's principle any equilibrium state nullifies the eff...
Text Solution
|
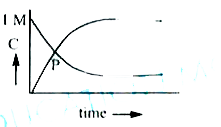
- At point P" of the reaction
Text Solution
|