Similar Questions
Explore conceptually related problems
Recommended Questions
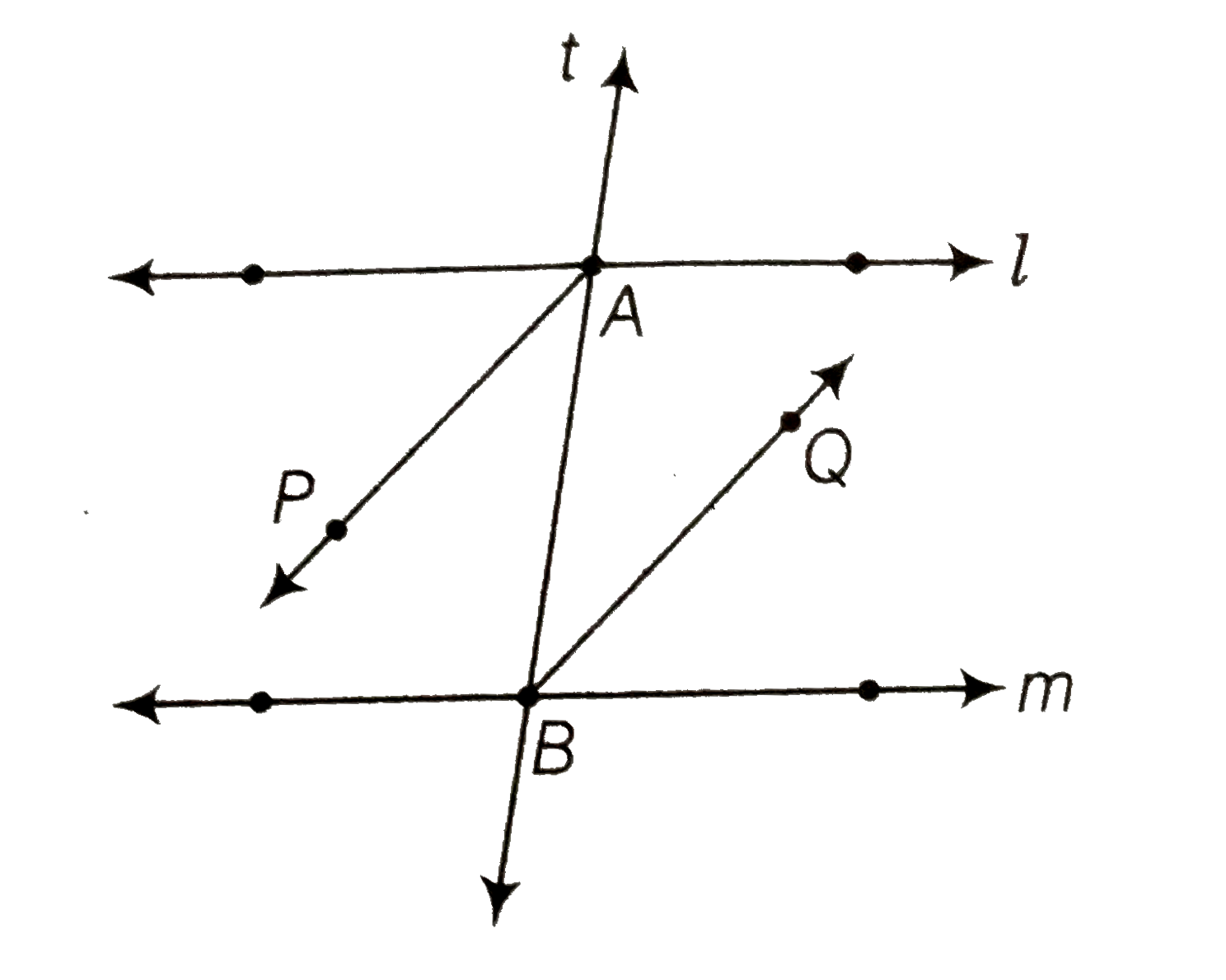
- AP and BQ are the bisectors of the two alternate interior angles forme...
Text Solution
|
- AP and BQ are the bisectors of the two alternate interior angles forme...
Text Solution
|
- In the given figure, bisectors AP and BQ of the alternate interior ang...
Text Solution
|
- How many lines of symmetry does the above figure have ? <img src="http...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Dtermine the images of the following figure about the given line : ...
Text Solution
|
- Draw the bisector of angleAOB=58^(@) ltimg src="https://d10lpgp6xz60...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|