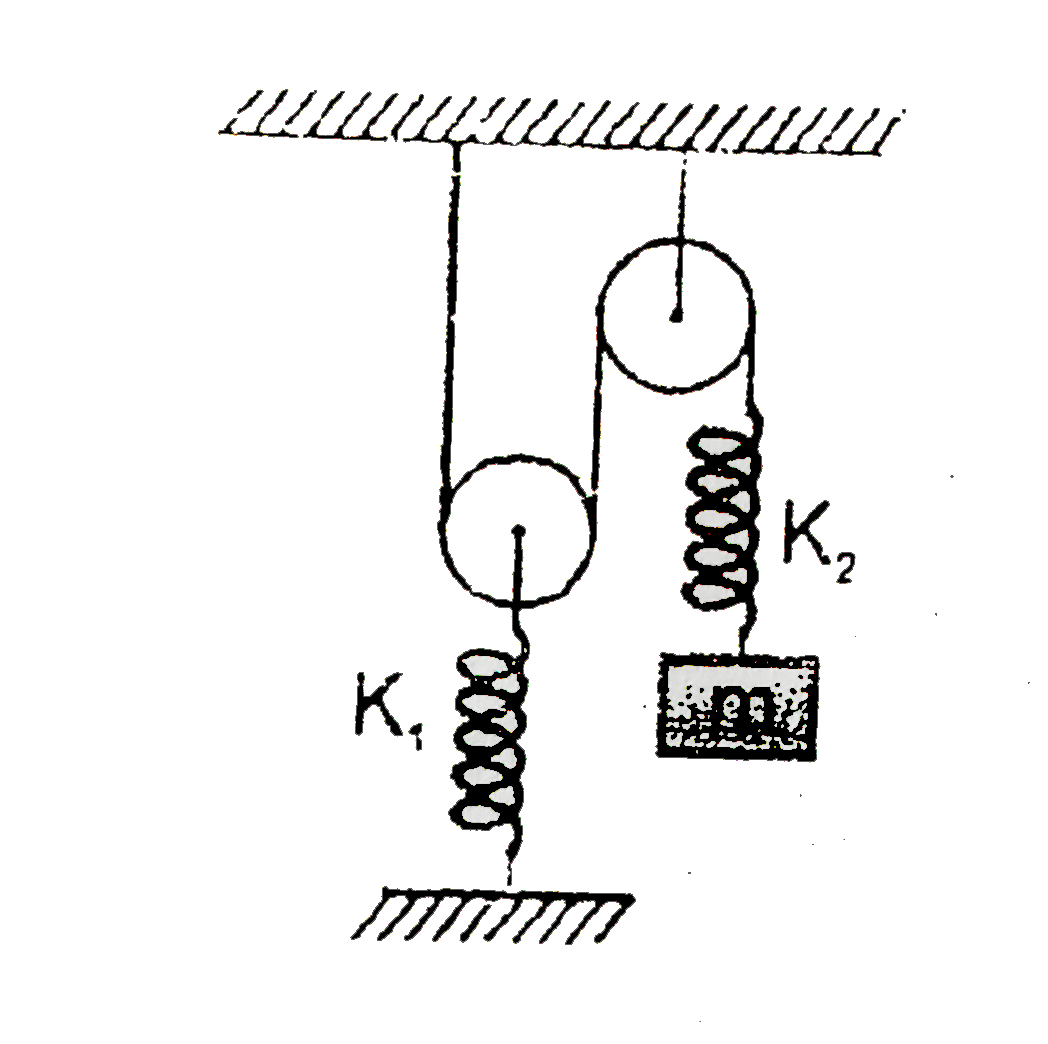Similar Questions
Explore conceptually related problems
Recommended Questions
- For given spring mass system, if the time period of small oscillations...
Text Solution
|
- A block of mass m hangs from a vertical spring of spring constant k. I...
Text Solution
|
- In the arrangement shown in figure, pulleys are light and spring are i...
Text Solution
|
- In the given spring block system if k = 25 pi^(2) Nm^(-1), find time p...
Text Solution
|
- Spring mass system is shown in figure. Find the elastic potential ener...
Text Solution
|
- For given spring mass system, if the time period of small oscillations...
Text Solution
|
- Spring mass system is shown in figure. Find the elastic potential ener...
Text Solution
|
- For given spring mass system, if the time period of small oscillations...
Text Solution
|
- Figure shows a system consisting of pulley having radius R, a spring o...
Text Solution
|