Similar Questions
Explore conceptually related problems
Recommended Questions
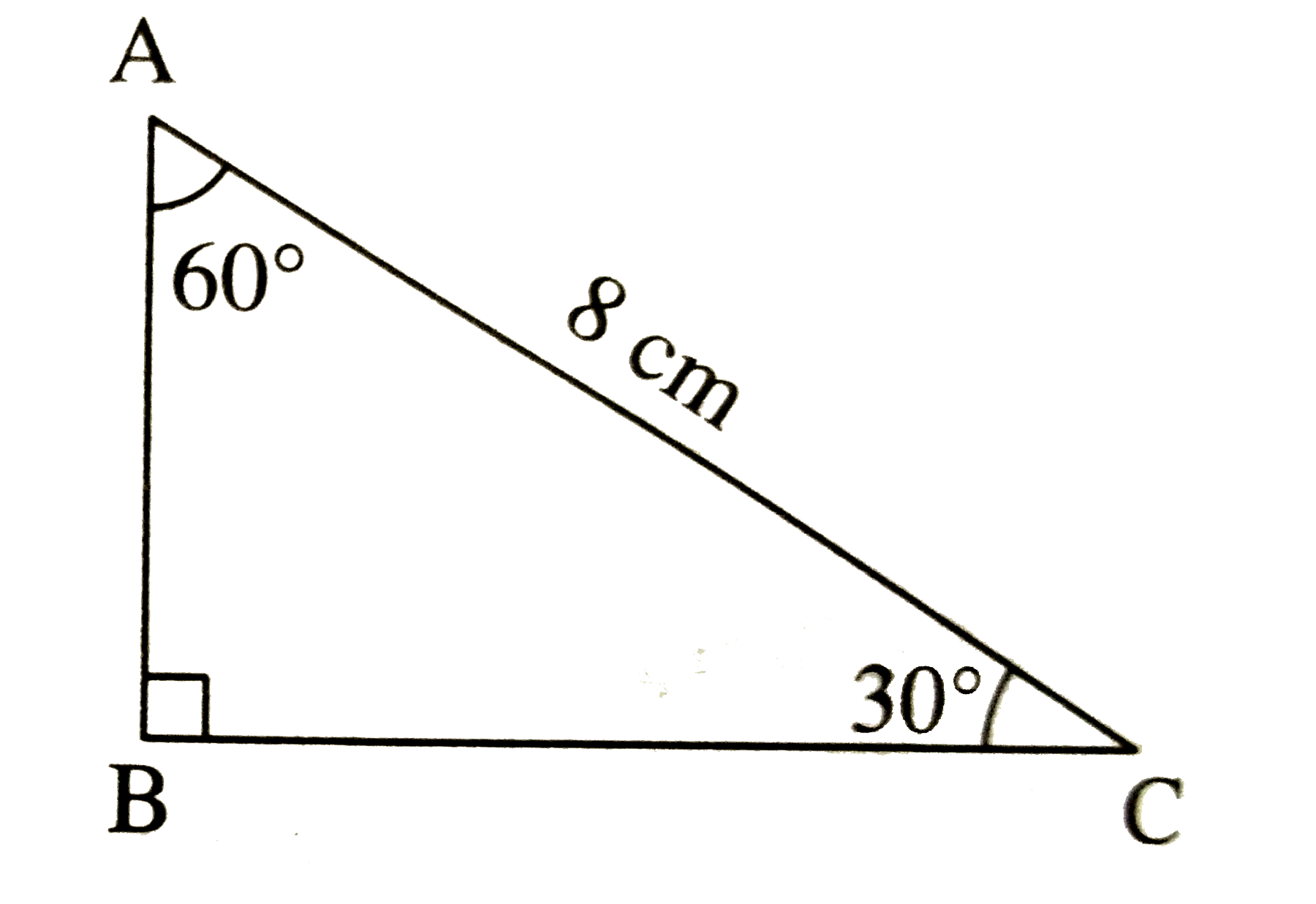
- In the figure, AC=8cm, /ABC=90^(@). /BAC=60^(@), /ACB=30^(@). Complete...
Text Solution
|
- In a right triangle ABC, < B =90^@. (a) If Ab=6cm,BC=8cm, find AC (b...
Text Solution
|
- In the figure above (not to scale), overline(AB)botoverline(CD) and AD...
Text Solution
|
- In a DeltaABC, angleB=90^(@) and AC=8sqrt(2). If AB=BC, then find AB.
Text Solution
|
- In the following figure, if the tension in the string AB is 51N, then ...
Text Solution
|
- In the figure, AC=8cm, /ABC=90^(@). /BAC=60^(@), /ACB=30^(@). Complete...
Text Solution
|
- In DeltaABC, AC=BC and /ACB=90^(@) then prove AB^(2)=2AC^(2)
Text Solution
|
- In Delta ABC, P,Q and R are midpoints of sides AB,AC and BC respectiv...
Text Solution
|
- In Delta ABC, AB | BC and /ACB=30^@ If AB=15m find BC
Text Solution
|