Similar Questions
Explore conceptually related problems
Recommended Questions
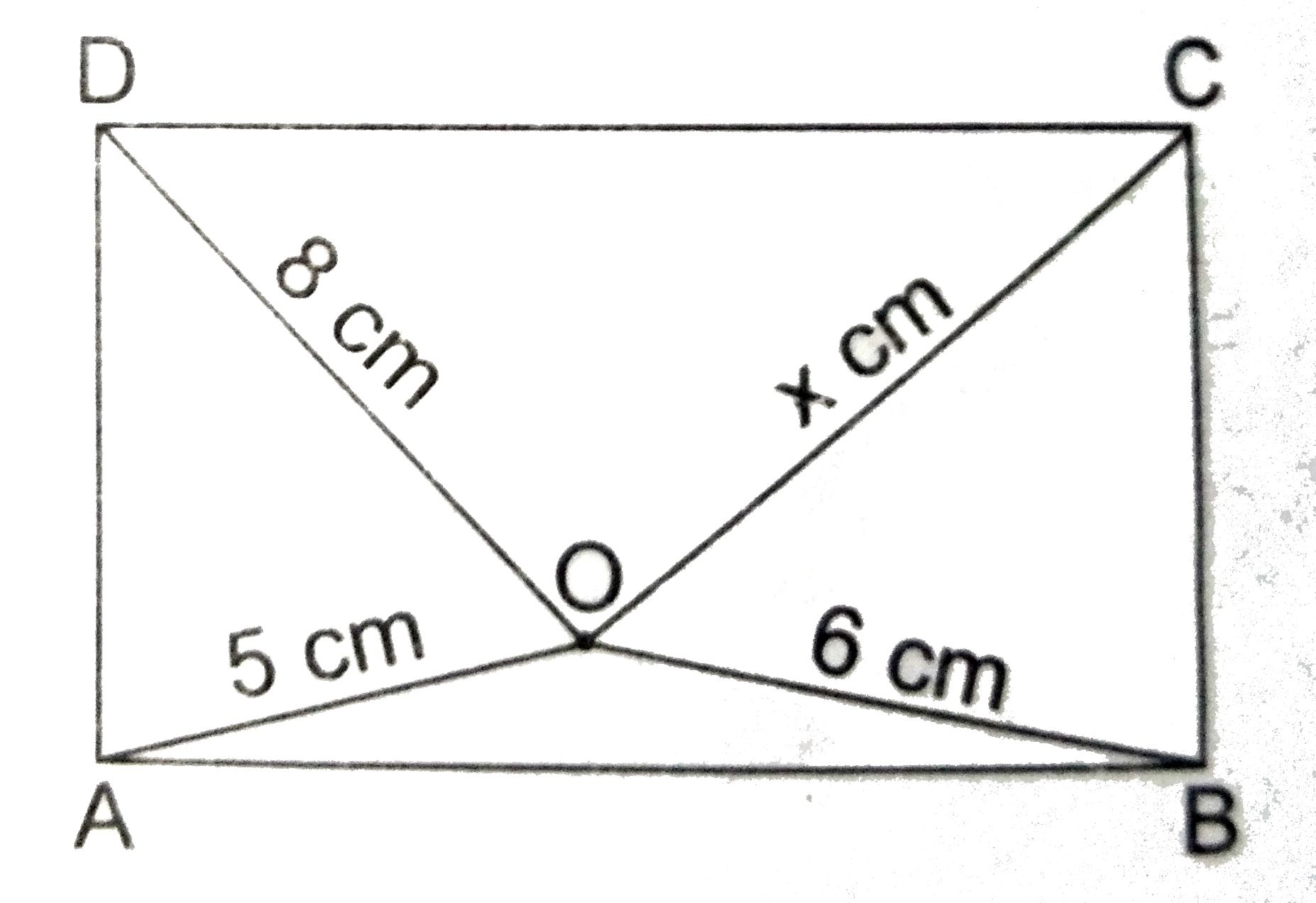
- O is any point inside a rectangle ABCD. Prove that OB^(2)+OD^(2)=OA^(2...
Text Solution
|
- आयत ABCD के अंदर स्थित O कोई बिंदु है सिद्ध कीजिए कि OB^(2)+OD^(2)=OA^...
Text Solution
|
- O is any point inside a rectangle ABCD. Prove that OB^(2)+OD^(2)=OA^(2...
Text Solution
|
- O is any point inside a rectangle ABCD, Prove that OA^(2) + OC^(2)= OB...
Text Solution
|
- In figure O is any point inside a rectangle ABCD. Prove that OB^(2)+OD...
Text Solution
|
- O' is any point inside a rectangle ABCD. Prove that OB^2+OD^2=OA^2+O...
Text Solution
|
- If 'O' is any point in the interior of rectangle ABCD, then prove that...
Text Solution
|
- படத்தில் O என்பது செவ்வகம் ABCD யில் உள்ளே உள்ள எனில் ,OB^2+OD^2=OA^2+...
Text Solution
|
- ‘O’ is any point inside a rectangle ABCD. Prove that OB^(2) + OD^(2) ...
Text Solution
|