Similar Questions
Explore conceptually related problems
Recommended Questions
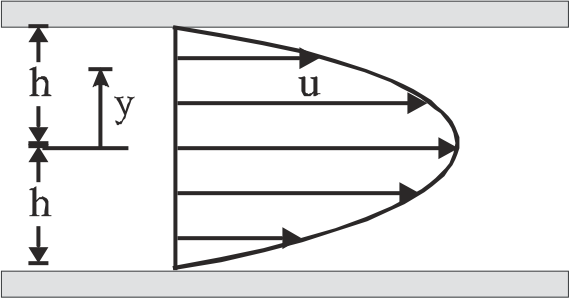
- The velocity distribution for the flow of a Newtonian fluid between tw...
Text Solution
|
- The velocity distribution for the flow of a Newtonian fluid between tw...
Text Solution
|
- The velocity distribution for the flow of a Newtonian fluid between tw...
Text Solution
|
- The velocity distribution for the flow of a Newtonian fluid between tw...
Text Solution
|
- A tube of length 1 and radius R carries a steady flow of fluid whose d...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|
- Viscosity is the property of fluid by virtue of which fluid offers res...
Text Solution
|