Similar Questions
Explore conceptually related problems
Recommended Questions
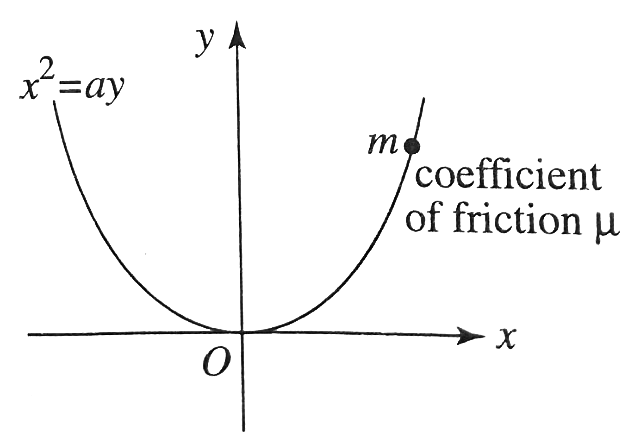
- A bead of mass m is located on a parabolic wire with its axis vertical...
Text Solution
|
- A bead of mass m is located on a parabolic wire with its axis vertical...
Text Solution
|
- A bead of mass m is located on a parabolic wire with its axis vertical...
Text Solution
|
- A piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis ve...
Text Solution
|
- A bead of mass m is located on a parabolic wire with its axis vertica...
Text Solution
|
- Angular velocity of smooth parabolic wire y = 4c(x^2) about axis of pa...
Text Solution
|
- A piece of wire is bent in the shape of a parabola y = kx^(2) (y-axis...
Text Solution
|
- Angular velocity of smooth parabolic wire y = 4c(x)^(2) about axis of ...
Text Solution
|
- A piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis ve...
Text Solution
|