Similar Questions
Explore conceptually related problems
Recommended Questions
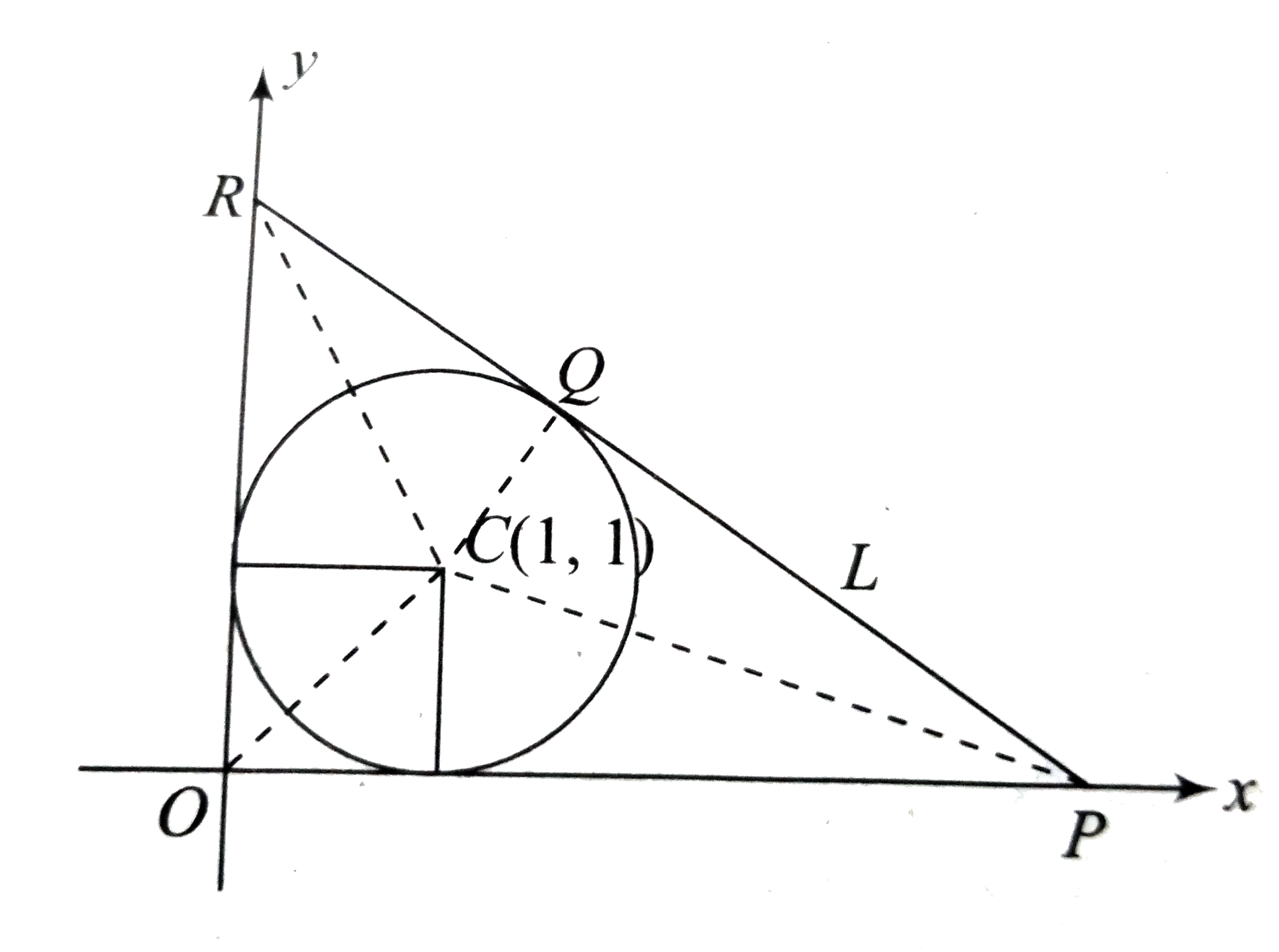
- In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
Text Solution
|
- In the diagram as shown, a circle is drawn with centre C(1, 1) and rad...
Text Solution
|
- How many lines of symmetry does the above figure have ? <img src="http...
Text Solution
|
- In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
Text Solution
|
- In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Complete adjectant figure so that X-axis and Y-axis are the lines of s...
Text Solution
|
- Dtermine the images of the following figure about the given line : ...
Text Solution
|
- In the given figure, AB is a diameter, O is the center of the circle ...
Text Solution
|