Recommended Questions
- Read the following passage carefully and answer the questions The...
Text Solution
|
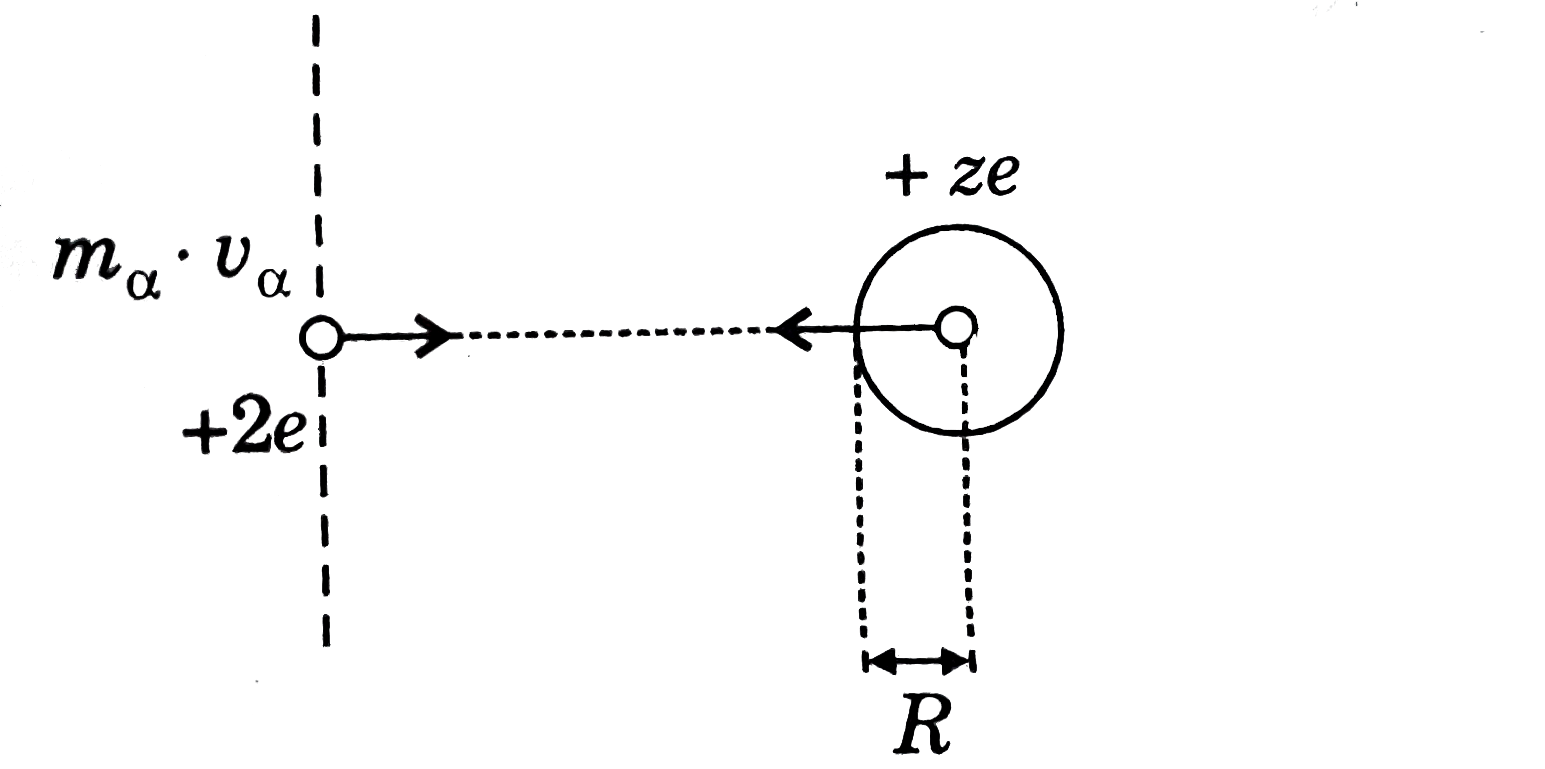
- An alpha particle having KE equal to 8.7MeV is projected towards the n...
Text Solution
|
- Read the following passage carefully and answer the questions The...
Text Solution
|
- Read the following passage carefully and answer the questions The...
Text Solution
|
- Read the following passage carefully and answer the questions The...
Text Solution
|
- What is the distance of closest approach to the nucleus for an alpha-p...
Text Solution
|
- What is the distance of closest approach to the nucleus of an alphapar...
Text Solution
|
- Rutherford model: The approximate size of the nucleus can be calculate...
Text Solution
|
- In Rutherford experiment alpha – particles are scattered by nucleus ha...
Text Solution
|