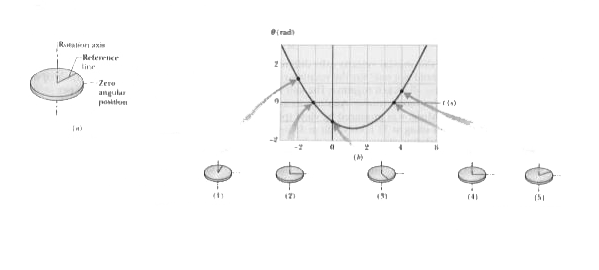
(a) The angular position of the disk is the angular position `theta(t)` of its reference line, which is given by a function of time t. So we graph, the result is shown in Fig.
Calculations: To sketch the disk and its reference line at a particular time, we need to determine `theta` for that time. To do so, we substitute the time. For t = -2.0 s, we get
`theta=-1.00-(0.600)(-2.0)+(0.250)(-2.0)^(2)`
= `1.2rad=1.2rad(360^(@))/(2pirad)=69^(@)`.
This means that at t = -2.0 s the reference line on the disk is rotated counterclockwise from the zero position by angle 1.2 rad = `69^(@)` (counterclockwise because `theta` is positive). Sketch 1 in Fig. shows this position the reference line.
Similarly, for t = 0, we find `theta=-1.00rad=-57^(@)`, which means that the reference line is rotated clockwise from the zero angular position by 1.0 rad, or `57^(@)`, as shown in sketch 3. For t = 4.0 s, we find `theta=0.60rad=34^(@)`. Drawing sketches for when the curve crosses the t axis is easy, because then `theta` = 0 and the reference line is momentarily aligned with the zero angular position.
(b) To find the extreme value of a function, we take the first derivative of the function and set the result to zero.
Calculations: The first derivative of `theta(t)` is
`(d theta)/(dt)=-0.600+0.500t`
Setting this to zero and solving for t give us the time at which `theta(t)` is minimum:
`t_(min)=1.20 s`.
To get the minimum value of `theta`, we next substitute `t_(min)` into Eq. finding
`theta=-1.36rad~~-77.9^(@)`.
This minimum of `theta(t)` corresponds to the maximum clockwise rotation of the disk from the zero angular position, somewhat more than is shown in sketch 3.
( c) From the angular velocity `omega` is equal to `d theta//dt` as given in Eq. So, we have
`omega=-0.600+0.500t`.
The graph of this function `omega(t)` is shown in Fig. Because the function is linear, the plot is a straight line. The slope is 0.500 `rad//s^(2)` and the intercept with the vertical axis is -0.600 rad/s.
Calculations: To sketch the disk at t = -2.0 s, we substitute that value into Eq., obtaining
`omega=-1.6rad//s`.
The minus sign here tells us that at t = -2.0 s, the disk is turning clockwise.
Substituting t = 4.0 s into Eq. given us
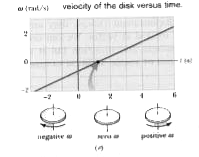
The implied plus sign tells us that now the disk is turning counterclockwise.
For `t_(min)`, we already known that `d theta//dt=0`. So, we must also have `omega=0`. That is, the disk momentarily stops when the reference line reaches the minimum value of `theta` in Fig. as suggested by the center sketch in Fig. On the graph of `omega` versus t in Fig. this momentary stop is the zero point where the plot changes from the negative clockwise motion to the positive counterclockwise motion.
(d) Description: When we first observe the disk at t = -3.0s, it has a positive angular position and is turning clockwise but slowing. It stops at angular position `theta=-1.36` rad and then begins to turn counterclockwise, with its angular position eventually becoming positive again.

