We are given the job of designing a large horizontal ring that will rotate around a vertical axis and that will have a radius of r = 33.1 m. Passengers will enter through a door in the outer wall of the ring and then stand next to that wall. We decide that for the time interval t = 0 to t = 2.30 s, the angular position `theta(t)` of a reference line on the ring will be given by
`theta=ct^(3)`,

with `c=6.39xx10^(-2)rad//s^(3)`. After t = 2.30 s, the angular speed will be held constant until the end of the ride. Once the ring begins to rotate, the floor of the ring will drop away from the riders but the riders will not fall - indeed, they feel as though they are pinned to the wall. For the time t = 2.20 s, let's determine a rider's angular speed `omega`, linear speed `nu`, angular acceleration `alpha`, tangential acceleration `a_(t)`, radial acceleration `a_(r)`, and acceleration `veca`.

Explanation

(1) The angular speed `omega` is given by Eq. `(omega=d theta//dt)`. (2) The linear speed `nu` (along the circular path) is related to the angular speed (around the rotation axis) by Eq. `(nu=omegar)`. (3) The angular acceleration `alpha` is given by Eq. `(alpha=domega//dt)`. (4) The tangential acceleration `a_(t)` (along the circular path) is related to the angular acceleration (around the rotation axis) by Eq. `(a_(t)=alphar)`. (5) The radial acceleration `a_(r)` is given Eq. `(a_(r)=omega^(2)r)`. (6) The tangential and radial accelerations are the (perpendicular) components of the (full) acceleration `veca`.
Calculations: Let.s go through the steps. We first find the angular velocity by taking the time derivative of the given angular position function and then substituting the given time of t = 2.20 s:
`omega=(d theta)/(dt)=d/dt(ct^(3))=3ct^(2)`
= `3(6.39xx10^(-2)rad//s^(3))(2.20s)^(2)`
= 0.928 rad/s.
the linear speed just then is
`nu=omegar=3ct^(2)r`
= `3(6.39xx10^(-2)rad//s^(3))(2.20s)^(2)(33.1m)`
= 30.7 m/s.
Next, let.s tackle the angular acceleration by taking the time derivative of Eq.
`alpha=(domega)/(dt)=d/dt(3ct^(2))=6ct`
= `6(6.39xx10^(-2)rad//s^(3))(2.20s)=0.843rad//s^(2)`.
The tangential acceleration then follows from Eq.
`a_(1)=alphar=6ctr`
= `6(6.30xx10^(-2)rad//s^(3))(2.20s)^(2)(33.1m)`
= `27.91m//s^(2)~~27.9m//s^(2)`.
or 2.8 g Eq. tells us that the tangential acceleration is increasing with time (but it will cut off at t = 2.30 s). From Eq, we write the radial acceleration as
`a_(r)=omega^(2)r`.
Substituting from Eq. leads us to
`a_(r)=(3ct^(2))^(2)r=9c^(2)t^(4)r`
= `9(6.39xx10^(-2)rad//s^(3))^(2)(2.20s)^(4)(33.1m)`
= `28.49m//s^(2)~~28.5m//s^(2)`,
or 2.9 g (which is also reasonable and a bit exciting).
The radial and tangential accelerations are perpendicular to each other and form the components of the rider.s acceleration `veca`. The magnitude of `veca` is given by
`a=sqrt(a_(r)^(2)+a_(t)^(2))`
= `sqrt((28.49m//s^(2))^(2)+(27.91m//s^(2))^(2))`
`~~39.9m//s^(2)`.
or 4.1 g (which is really exciting). All these values are acceptable.
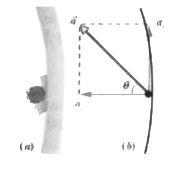
To find the orientation of `veca`, we can calculate the angle `theta` shown in Fig.
`tantheta=a_(t)/a_(r)`.
However, instead of substituting our numerical results, let.s use the algebraic results from Eq.
`theta=tan^(-1)((6ctr)/(9c^(2)t^(4)r))=tan^(-1)(2/(3ct^(3)))`.
The big advantage of solving for the angle algebraically is that we can then see that the angle (1) does not depend on the ring.s radius and (2) decreases as t goes from 0 to 2.20 s. That is, the acceleration vector `veca` swings toward being radially inward because the radial acceleration (which depends on `t^(4)`) quickly dominates over the tangential acceleration (which depends on only t). At our given time t = 2.20 s, we have
`theta="tan"^(-1)2/(3(6.39xx10^(-2)rad//s^(3))(2.20s)^(3))=44.4^(@)`.