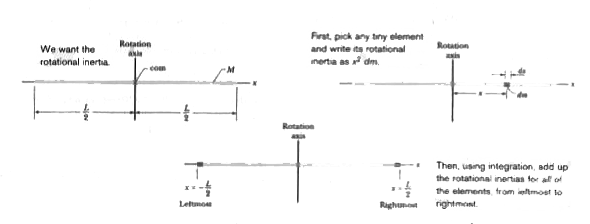
(a) (1) The rod consists of a huge number of particles at a great many different distances from the rotation axis. We certainly do not want to sum their rotational inertias individually. So, we first write a general expression for the rotational inertia of a mass element dm at distance r from the rotation axis: `r^(2)`dm. (2) Then we sum all such rotational inertias by integrating the expression.
`I=intr^(2)dm`.
(3) Because the rod is uniform and the rotation axis is at the center, we are actually calculating the rotational inertia `I_(com)` about the center of mass.
Calculations: We want to integrate with respect to coordinate x, so we must relate the mass dm of an element of the rod to its length dx along the rod. Because the rod is uniform, the ratio of mass to length is the same for all the elements and for the rod as a whole. Thus, we can write.
`("element.s mass dm")/("element.s length dx")=("rod.s mass M")/("rod.s length L")`
or `dm=M/Ldx`.
We can now substitute this result for dm and x for r in Eq. Then we integrate from end to end of the rod (from x = -L/2 to x = L/2) to include all the elements.
`I=int_(x=-L//2)^(x=+L//2)x^(2)(M/L)dx`
= `M/(3L)[x^(3)]_(-L//2)^(+L//2)=M/(3L)[(L/2)^(3)-(-L/2)^(3)]`
= `1/12ML^(2)`
(b) We can find I by shifting the origin of the x axis to the left end of the rod and then integrating from x = 0 to x = L. However, here we shall use a more powerful technique by applying the parallel-axis theorem, in which we shift the rotation axis without changing its orientation.
Calculations: If we place the axis at the rod.s end so that it is parallel to the axis through the center of mass, then we can use the parallel-axis theorem. We know from part (a) that `I_(com)` is 1/12 `ML^(2)`. From Fig. the perpendicular distance h between the new rotation axis and the center of mass is 1/2 L. Equation given us
`I=I_(com)+Mh^(2)=1/12ML^(2)+(M)(1/2L)^(2)`
= `1/3ML^(2)`.
