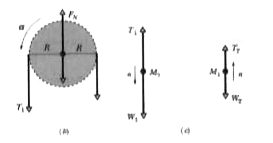
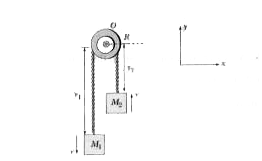
(1) If the block `M_(1)` moves upward, the block `M_(2)` moves downward, and the pulley will rotate counterclockwise. This problem is same as Sample Problem we have already solved, except that now we have to use angular momentum and torque to find acceleration.
(2) We define the blocks and pulley as our system. We consider the axle of the pulley as our axis. We can write the angular momentum of the system considering the ball and the block that are moving translationally and the pulley which is undergoing pure rotation. The external torque on the system about the axis is due to the weights of the blocks.
Calculations: Due to constraint, the blocks have same speed n. We can find angular momentum using the definition of angular momentum about the axle, given by equation `vecL=vecrxxvecp`.
The momentum and position vectors are given by
`vecP_(1)=-M_(1)nuhatjandr_(1)=-Rhati-y_(1)hatj`
Using `vecL=vecrxxvecp`, the angular momentum of block 1 is `M_(1)nuRhatk`.
Similarly, for block 2, momentum and position vectors are given by
`vecP_(2)=+M_(2)nuhatjandr_(1)=Rhati+y_(2)hatj`
Using `vecL=vecrxxvecp`, the angular momentum of block 2 is `M_(2)nuRhatk` about our chosen axis.
The angular momentum of the pulley can be found using `L=Iomega`. It is given by `M_(p)R^(2)omegahatk//2` about our chosen axis.
We calculate the external torque acting on the system about the pulley axle. The force is being exerted by the axle on the pulley, but it does not produce torque about the axle as the length of moment arm is zero.
The gravitational force `M_(1)vecg` acting on block 1 produces a torque about the axle equal to `M_(1)gRhatk` and the gravitational force `M_(2)vecg` acting on block 2 produces a torque about the axle equal in magnitude to `-M_(2)gRhatk`, where R is the moment arm of the force about the axle. Thus, the total external torque about the pulley axle is
`sumtau_(ext)=M_(1)gRhatk-M_(2)gRhatk`
Writing an expression for the total angular momentum of the system,
`L=(M_(1)nuR+M_(2)nuR+MnuR)hatk`
Substituting this expression and the total external torque in
`sumt_(ext)=(dL)/(dt)`
`M_(1)gRhatk-M_(2)gRhatk=d/dt[(M_(1)+M_(2)+M)nuR]hatk`
`M_(1)gR-M_(2)gR=(M_(1)+M_(2)+M)R(dnu)/(dt)`
Recognizing that `dnu//dt=a` and solving Eq. for a
`a=((M_(1)-M_(2))g)/(M_(1)+M_(2)+M)`