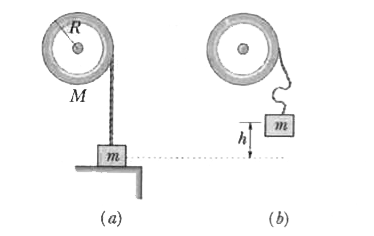
A horizontal, homogeneous cylinder of mass M and radius R is pivoted about its axis of symmetry. A string is wrapped several times around the cylinder and tied to a body of mass m resting on a support positioned so that the string has no slack. The body of mass m is then lifted vertically to a distance h, and then released.
(a) Evaluate the angular velocity `omega_(0)` of the cylinder, the speed `v_(0)` of the falling body of mass m, and the kinetic energy `K_(0)` of the system, just before the string becomes taut.
(b) Evaluate the corresponding quantities, `omega_(1),v_(1),andK_(1)`, for the instant just after the string becomes taut.

Explanation

(a) Since string is slack we can expect that the block will fall freely for distance l. Till this time tension in string will be zero.
Calculation: Just before the string becomes taut, the cylinder is still at rest. Since the tension remained zero nothing has caused the cylinder to begin turning. That is, `omega_(0)=0`. Since the string has exerted no force on the body of mass m, it has fallen freely with acceleration g thus `v_(0)=2gh`. Same result can be derived by writing

work-kinetic energy theorem for the system. The kinetic energy of the system is given by
`K_(0)=1/2mv_(0)^(2)+1/2I_(C)omega_(0)^(2)=mgh`
where `I_(c)` is the inertia of the cylinder.
Putting `omega_(0)=0`, we get
`v_(0)=sqrt(2gh)`
(b) (1) The end attached to the block will be moving and it will pull the part of string touching the cylinder as the string becomes taut. (2) Thus, when string becomes tight an impulse/jerk will develop in the string. This jerk will start the motion of cylinder. There will be also an impulse due to axis of the cylinder. Here we can take cylinder, string and clock as our system. We will take axle of cylinder as the axis for writing angular momentum.
Calculations: The impulse due to jerk in string will produce internal angular impulse, and the impulse due to the angular momentum will produce zero angular impulse about the axle. Further, the angular momentum of the system must be conserved, since the impulse due to the snap of the string is of very short duration and the weight mg contributes negligibly in that time. The string is assumed to be inextensible, so `v_(1)=omega_(1)R`.
Thus, we have `L_(1)=mv_(1)R+(1//2)MR^(2)omega_(1)=L_(0)`, where `L_(0)=mv_(0)R=msqrt(2gh)R`. Solving for the angular speed, we get
`omega_(1)=v_(0)/(R[1+(M//2)m))=sqrt(2gh)/(R[1+((M//2)m)])`
The corresponding speed is given by
`v_(1)=omega_(1)R=v_(0)/(1+((M//2)m))=(sqrt(2gh))/([1+((M//2)m)])`
The final kinetic energy `K_(1)` is given by
`K_(1)=1/2mv_(1)^(2)+1/2I_(c)omega_(1)^(2)=mgh`
= `1/2mv_(1)^(2)+1/2(1/2MR^(2))`
`(v_(1)^(2)/R^(2))=1/2(m+M/2)v_(1)^(2)`
= `1/2((mv_(0)^(2))/(1+((M//2)m)))`