Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-OSCILLATIONS-Additional Exercises
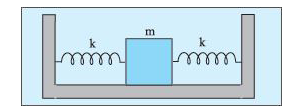
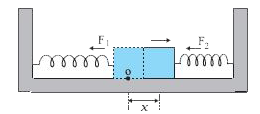
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- An air chamber of volume V has a neck area of cross section a into whi...
Text Solution
|
- You are riding in an automobile of mass 3000 kg. Assuming that you are...
Text Solution
|
- Show that for a particle in linear SHM the average kinetic energy over...
Text Solution
|
- A circular disc of mass 10 kg is suspended by a wire attached to its c...
Text Solution
|
- A body describes simple harmonic motion with an amplitude of 5 cm and ...
Text Solution
|
- A mass attached to a spring is free to oscillate, with angular velocit...
Text Solution
|